一、宇宙观的演变

赵凯华

（一）从哥白尼到开普勒

在科学不发达的古代，人们已开始对宇宙的结构产生种种的设想和猜测。在中国有盖天、浑天、宣夜诸说；在希腊，从亚里士多德到托勒玫，数百年间建立起极为精致的宇宙模型。那时在人们的观念里，毫无例外地把人类自己放在宇宙的中心。

公元150年前后托勒玫（C. Ptolemy）把当时已发展得异常之好的天文学知识（精度惊人的观测数据）总结成宇宙的地心体系（图1），在此体系中太阳、月亮和各行星都固着在不同的水晶天球上绕地球旋转，恒星则呆在最外的天球上。行星在天球上的视轨迹是相当复杂的。最引入注目的特征是，在恒星的背景上行星有时要逆行（retrograde，见图2）。托勒玫的体系把每个行星的运动描绘成沿一个称为本轮（epicycle）的小圆回转，而本轮的中心又循着以地球为中心的一个称为均轮（deferent）的大圆运行。这就解释了且不管人们的宇宙观如何，行星的逆行问题（见图3）。

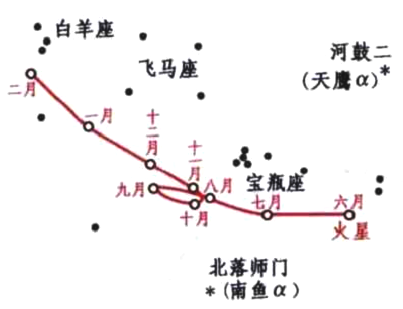
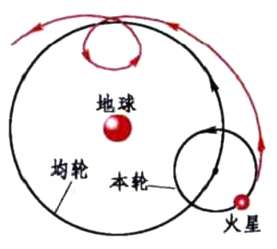
为了使其理论体系与相当精确的天文观测数据吻合，托勒玫在本轮上再加一层又一层的本轮。尽管这个体系变得非常复杂，它却能给出行星以前的轨迹，并能相当好地预言它们未来的位置，于是，托勒玫体系一代代传下来，直到15世纪，未发生重大变化。

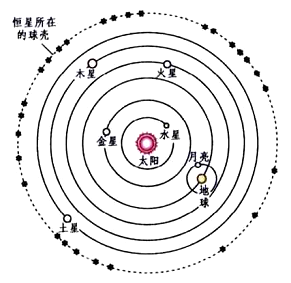
哥白尼（Nicolaus Copernicus）1473年生于波兰，他对托勒玫庞杂的大小本轮体系强烈地不满，哥白尼认为，如果把太阳放在中心，对行星运动的描述将会大大简化。图4是哥白尼的日心体系，在这个体系中，五大行星和地球都绕着太阳作圆周运动。哥白尼的学说与天主教的教义严重抵触，遭到了教廷的封杀。

布鲁诺（Giordano Bruno）不是天文学家，他通过哲学思辨主张宇宙无限的观念。虽然哥白尼的宇宙体系保留了恒星天球，仍是一个有限的体系，布鲁诺把哥白尼的日心说发展成一个无限的体系，在欧洲大陆和英国宣传哥白尼的日心说。1600年被罗马教廷烧死在鲜花广场上。

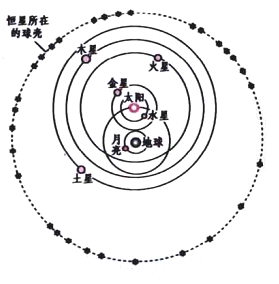
第谷•布拉赫（Tycho Brahe）1583年提出了一个混合体系（见图5），仍把地球安置在宇宙的中心，五颗行星则绕太阳转，而太阳带着它们围绕地球运行。布拉赫体系在不涉及恒星天时与哥白尼体系在数学上是等价的，他的体系和观测都驱使他的追随者转向哥白尼阵营。

开普勒（Johannes Kepler）是布拉赫的助手，他与布拉赫相比更倾向于理论上的思考。布拉赫死后，他把自己的全副精力用来整理布拉赫的观测数据，企图求得行星运行轨道的最简单描述，出于便于观测的原因，他详细研究了火星的运动。

在研究火星运动轨道的过程中，开普勒总结出行星运动的等面积定理：设想从太阳向行星引一条辐线（径矢），他发现这条辐线在相等的时间间隔内扫过相等的面积（见图6）。为了拟合出行星的轨道，开普勒开始也是用本轮—均轮的方法（不过把太阳放在中心），但不成功；于是他放弃了匀速圆周运动这个一向为人们钟爱的古老信念，着手用卵形线去拟合行星轨道，经过详细计算，最后，他发现，用椭圆轨道才能精确地拟合行星的轨道，而太阳处在它的一个焦点上（见图6），这就是开普勒1609年发表的第一定律，而面积定理则成为他的第二定律。

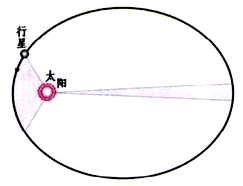
古希腊以来，人们就想到，行星的轨道愈大，绕行一周的时间（周期）愈长。开普勒进一步的努力找出了二者之间的定量关系：椭圆轨道的半长轴a与周期T的2/3次方成正比，这便是开普勒1618年完成的第三定律。

开普勒三定律归纳如下：

（1）行星沿椭圆轨道绕太阳运行，太阳位于椭圆的一个焦点上。

（2）对任一个行星说，它的径矢在相等的时间内扫过相等的面积。

（3）行星绕太阳运动轨道半长轴a的三次方与周期T的二次方成正比。

开普勒获此结果欣喜若狂，他毫不掩饰地说：“十六年了，我立志要探索一件事，所以我和第谷结合起来，……我终于走向光明，认识到的真理远超出我最热切的期望。如今木已成舟，书已完稿，至于是否现在就有读者，抑或将留待后世？既然上帝已等了观察者六千多年，那么我也许要整整等上一个世纪才会有读者，对此我一点也不在乎。”

把二十余年里观测的几千个数据归纳成这样简洁的几条规律，开普勒是应该为此而感到自豪的。只是开普勒尚不理解，他所发现的三大定律已传达了重大的“天机”：角动量正比于径矢的掠面速度，故开普勒第二定律意味着角动量守恒，亦即行星受到的是有心力；此外，开普勒第三定律意味着引力的平方反比律。开普勒定律蕴涵着更为简洁、更为普遍的万有引力定律，个中的奥秘直到牛顿才被破译出来。

（二）伽利略的功勋

伽利略（Galileo Galilei）是近代物理学之父，他的努力对宣传、解释和捍卫哥白尼的日心说起了不可磨灭的作用。1608年荷兰的眼镜匠利帕希造出了第一架望远镜，第二年伽利略知道这个消息后自己动手制造了一架望远镜，放大倍率为20。用这架望远镜伽利略发现了月亮上的环形山和木星的四颗卫星（1610）。以及在太阳表面移动着的黑子（1612。见图7）。木卫绕着木星转，太阳也在自转，并非一切都围着地球转，这些新天象都不利于地心说。

伽利略最伟大的著作是他从1624～1630年花了6年时间写成的《关于托勒玫和哥白尼两大世界体系的对话》（图8）。书中阐明了现在称之为“伽利略相对性原理”的道理，用物体的惯性运动反驳了亚里士多德派对地动说的责难。该书1632年才侥幸获得教会批准而于3月出版，但8月即遭查禁，伽利略本人也遭到传讯。次年被判终身软禁。346年后。1979年罗马教皇保罗二世提出为伽利略平反。1980年正式宣布当年教会压制伽利略的意见是错误的。虽然这个迟到的决定已起不了什么实际作用，毕竟证明了真理是不可战胜的。

（三）牛顿的万有引力定律

下一个问题是什么原因使行星绕日运转？在开普勒时代有些人对此的回答是小天使在后面拍打翅膀，推动着行星沿轨道飞行。与此同时，伽利略发现了伟大的惯性定律，即不受任何作用的物体将按一定速度沿直线前进。再下一个问题是牛顿提出的，物体怎样才会不走直线？牛顿的回答是：以任何方式改变速度都需要力，所以，小天使们不应在后面，而应在侧面拍打翅膀，朝太阳的方向驱赶行星，换句话说，使物体作圆周运动，需要有个向心力。

牛顿之前虽有人推导过向心力公式，但不普遍。牛顿自己推导了现在我们熟知的向心力公式：

\(f = \frac{{m{v^2}}}{r}\)，

对于圆轨道，v＝2πr/T （T为周期），从而

\(f = \frac{{4{\pi ^2}mr}}{{{T^2}}}\)。

另一方面，按照开普勒第三定律，r³/T² ＝K（与行星无关的太阳系常量，叫做开普勒常量），则1/T² ＝K/r³ ，于是

\(f = \frac{{4{\pi ^2}mK}}{{{r^2}}}\)。

亦即，开普勒第三定律含有这样的内容：一个行星所受的向心力与其质量成正比，与它到太阳的距离平方成反比，平方反比的思想在牛顿之前就有，不过在没有牛顿创立的力和质量的确切概念之前，这种思想是含糊不清的。

牛顿“苹果落地”的故事广泛流传，这故事出自牛顿的亲友对他晚年谈话的回忆。故事大意是，1665～1666年间因瘟疫流行，牛顿从剑桥回到家乡，当时他正在思考月球绕地球运行的问题，一日他在花园中冥思重力的动力学问题时，看到苹果偶然落地，引起他的遐想：在我们能够攀登的最远距离上，在最高建筑物的顶上和最高山巅上，都未发现重力明显地减弱，这个力必定延伸到比通常想像远得多的地方。为什么不会高到月球上？如果是这样，月球的运动必定受到它的影响，或许月球就是由于这个原因，才保持在它的轨道上的。当然，尽管在地表的各种高度上重力没有明显地减弱，但是很可能到了月球那样高时，这个力在强度上会与我们这里很不相同。

如果知道月亮到地心的距离r_月地。从月球绕地的周期T＝27.3d≈2.36×10⁶s可以估算出月球绕地运行的向心加速度g_月：

\({g_月} = \frac{{{v^2}}}{{{r_月地}}} = \frac{{{{(2\pi {r_月地}/T)}^2}}}{{{r_月地}}} = \frac{{4{\pi ^2}{r_月地}}}{{{T^2}}}\)。

如果地球对它们的吸引力与距离的平方成反比的话。g_月与地面上苹果的重力加速度g＝9.8m/s²之比应等于地球半径R地与r月地之比的平方。天文学上相当精确地估算出r_月地/R_地 ＝60。故g_月/g应等于1/60²＝1/3600。但牛顿当时不知道R_地或r_月地的准确数值，因而未能令人满意地作出地心引力的月地检验，这可能是牛顿推迟了20年才发表万有引力定律的原因之一。此外还有一些问题有待解决。其中一个问题是地球对地面上物体（苹果）引力的距离为什么要从地心算起？此外，上面从向心力公式和开普勒第三定律导出平方反比关系，只适用于圆轨道，实际上行星的轨道是椭圆的。牛顿直到1684年才用相当复杂的几何方法明确地将这些问题解决（图9）。

从苹果落地到月地检验，讨论的是地球的引力；行星运动问题讨论的是太阳的引力，牛顿在1665年到1685年的20年里，把引力的思想不断扩大，最后概括出“万有引力”的概念来：

……如果由实验和天文学观测，普遍显示出地球周围的一切天体被地球重力所吸引，并且其重力与它们各自含有的物质之量成正比，则月球同样按照物质之量被地球重力所吸引。另一方面，它显示出，我们的海洋被月球重力所吸引；并且一切行星相互被重力所吸引，彗星同样被太阳的重力所吸引。由于这个规则，我们必须普遍地承认，一切物体，不论是什么，都被赋予了相互引力的原理。因为根据这些表象所得出的物体的万有引力的论证，要比它们的不可入性的论证有力得多……（《自然哲学的数学原理》）。

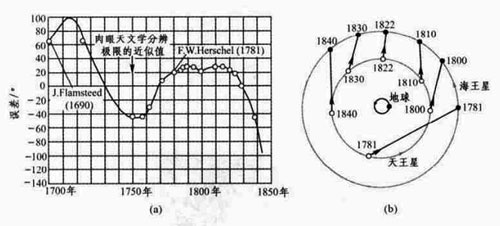
预见并发现从未想到过的行星，也许是万有引力理论威力最生动的例证。1781年赫歇耳（F.W.Herschel）偶然发现天王星，并在早先的一些星图中把它认了出来，发现1690年以后已有关于它的记录。把这些记录与几个月中进行的新测量结合起来，就证明这天体确是我们太阳系的一员，走着一个差不多是圆形的轨道，平均半径为19.2AU（1AU＝1.496×10¹¹m），周期为84年。此后天王星的运动就成为不断研究的主题。积累的数据表明，它的运动有某些极小的不规则性，这些不规则性不能归因于已知来源的摄动效应（见图10（a））。这种反常使人们怀疑，在天王星外还有另一颗未知的行星。英国的亚当斯（J.C.Adams）和法国的勒威耶（U.Le Verrier）独立地对此进行了工作，根据一个被称为“博德定律”的经验公式，假定这颗未知行星轨道半径约为天王星的两倍，再从开普勒第三定律算出其周期，即可画出如图10（b）所示的一幅明确图像，说明这新行星如何按其相对位置交错地使天王星在其轨道运动中加速和减速。通过细致的分析，人们可以计算出这颗新行星在什么时日出现在什么方位，亚当斯于1845年10月向英国皇家天监提供了情报，未获积极的反应，勒威耶直到1846年8月才完成计算，致信德国天文学家伽勒（J.C.Galle），伽勒立即进行探索，在他第一夜的观测中就认出了那颗新行星。与预计的位置只差1°。海王星就这样在笔尖下被发现了。虽然这发现带有一定的机遇和偶然性，因为他们所用的博德公式并不对，但海王星的发现仍不失为牛顿动力学和万有引力定律最成功的例证。1930年汤姆博夫（C.W.Tambaugh）根据海王星自身运动不规则性的记载发现了冥王星，可说是前一成就的历史回声。

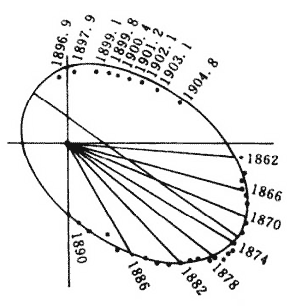
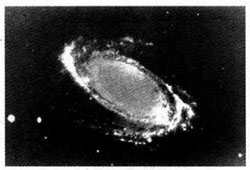
我们看到，万有引力理论在太阳系内获得极大的成功。它的威力究竟能够延伸到多远？在恒星世界中双星系统是很典型的，图11给出三张双星系克鲁格60在前后12年间相对位置变化的照片，图12是它们在天球上运行的详细记录。这系统大概离我们有10光年远，周期为44年，两伙伴之间的距离约为10AU。图11中展示的椭圆轨道使我们相信万有引力也在那里起作用，中心不在焦点上是因为轨道面相对于我们的视线倾斜的缘故。图13是一张涡旋星系的照片，从密度的径向分布我们还能大体上验证平方反比律是否成立，对于更大的结构，如星系团和超星系团，就不容易作定量的考察了。不过我们相信，那里也有引力在起作用，使物质逐渐凝聚起来。当今牛顿万有引力理论的新版本——广义相对论已成为现代天体物理学和宇宙学分析问题的基础，万有引力理论的普适性超越了宇宙的边缘！就这样，从苹果到月亮，从太阳到宇宙，上穷碧落下黄泉，天上人间，凡有引力参与的一切复杂现象，无不归结到一条简洁的定律中。还有什么比这更美妙的吗？

（四）宇宙学原理

秋夜仰望辽阔的星空，我们可以看到一条银白色的光带环绕天球，那就是银河。

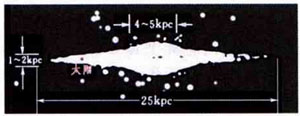
18世纪中叶人们已经意识到，满天星斗（恒星）都是远方的“太阳”。赫歇耳父子（F.W.Herschel和J.F.Herschel）在全天恒星观测和恒星计数方面做出了巨大贡献。1785年老赫歇耳曾根据恒星计数的统计研究，绘制了一幅扁而平、轮廓参差的银河系（Galaxy）结构图，在这个银河系构想里太阳居其中央，沙普利（H. Shapley）1918年建立了银河系的透镜模型（图14）。在此模型中，太阳已不在中心。20世纪20年代沙普利的模型为天文界所公认。

早在18世纪，人们在夜晚天空中发现了模糊的延展天体，最初统称为星云（nebulae）。其中涡旋星云成为最早引入注目的研究对象，康德等人就曾提出，涡旋星云可能是如我们的银河系一样的恒星系统。这就是所谓“岛宇宙假说”。反对岛宇宙假说的观点则认为，涡旋星系是银河系内的气体星云，围绕这个假说长期存在着争论，问题的症结是那个天文上最困难的问题——距离的估计，即涡旋星系究竟离我们有多远？这里需要一把可靠的“量天尺”。

造父变星（Cepheids）是一类亮度作周期性变化的超巨星，它的典型代表是仙王座δ星，中文名造父一。1908年哈怫大学天文台的女天文学家勒维特（H.Leavitt）小姐发现小麦哲伦云（一个与我们的银河系邻近的星系）内一些造父变星的周期和光度之间有明确的关系。由于小麦哲伦云本身的尺度比起它到我们的距离小得多，它里面的恒星到地球的距离可以看作大致相等。所以可以认为，小麦哲伦云里造父变星彼此之间表观的相对亮度，反映了它们之间的绝对亮度。也就是说，所有周期相同的造父变星，其真实亮度都相同。这样一来，我们就可以通过那些距离已知的造父变星的周期，来推算周期相同的造父变星的距离。所以，若能经过“校准”，造父变星将成为一把非常有力的“量天尺”，在勒维特的发现之后，一些天文学家利用本星系中可用三角视差法测量距离的造父变星，校准了这把量天尺，使得哈勃于20年代结束了那场“岛宇宙”之争。到了50年代，天文学家发现，造父变星有两类，各自有不同的周期—光度关系。勒维特在小麦哲伦云中研究过的造父变星，与我们银河系中曾用来校准量天尺的造父变星原属不同的类型。把这个错误纠正过来后，人们发现，宇宙的尺度一下子扩大了一倍多。

1923年，美国天文学家哈勃（E.P.Hubble）用当时世界上最大的望远镜将仙女座星云M31的外围部分分解为单个恒星，并认证出其中有造父变星，由它们的周期—光度关系归算出来的M31距离比我们的银河系直径大几百倍。因此确定M31和我们的银河系一样，是个独立的恒星系统——河外星系（galaxy）.这一来，人们的视野大大地开阔了，原来在我们的银河系之外有无数个河外星系，宇宙比人们当初想像的不知大了多少倍！

从图14所示，我们的星系——银河系尺度为25kpc。pc是“秒差距”，1pc≈3光年≈3×10¹⁶m。kpc为千秒差距（10³pc），Mpc为兆秒差距（10⁶pc）。银河系外各星系在空间是怎样分布的？由于万有引力是长程力，在很大距离上物质都有凝聚的倾向，星系在空间的分布不是均匀的，而是结成一团一团的，叫“星系团”。星系团由几百个上千个星系组成，其尺度为10Mpc。星系团在空间的分布也不太均匀，故有更大尺度的“超星系团”之说。如果我们把恒星看成宇宙中的气体分子，则在“宏观”尺度下其平均密度应该是均匀的。这里的区别是分子间的范德瓦尔斯力是短程力，而恒星间的万有引力是长程力。如果用相对密度涨落作为均匀性的量度，则在宇宙这个“分子气体”中相对密度涨落随空间尺度的增大而递减要比普通分子气体慢得多，观测表明，在12Mpc的尺度下平均看相对密度涨落的数量级为1。即宇宙绝对是不均匀的；在60Mpc的尺度下平均看相对密度涨落，其数量级降为10%。即宇宙有走向均匀的趋势。我们可以认为，大约在100Mpc，即10²⁴m的尺度上看，宇宙是均匀各向同性的。我们把这个空间尺度叫“宇观尺度”，大多数字宙学家认为如下的假设是合理的：

在宇观尺度下，任何时刻三维宇宙空间是均匀各向同性的。

这假设称为“宇宙学原理”。或“哥白尼原理”。这原理意味着，在宇观尺度上，宇宙中所有地点的观察者都是平权的。

哥白尼原理当然不是哥白尼提出来的。在古代人们的观念里，毫无例外地把人类自己放在宇宙的中心，历史上，是哥白尼率先否定了地心说，把宇宙的中心移到太阳上。随着天文学的发展，人们了解到，与银河系内许许多多的恒星一样，太阳也不过是一颗普普通通的恒星，它并不占据银河系的中心位置。后来天文上又发现，我们的银河系与许许多多的河外星系一样，也不过是一个普普通通的星系。宇宙观发展的历史，其实就是人类（或者说地球）逐渐从宇宙中心的宝座上一步步退下来的历史。从人类以自我为中心到多中心，最后到没有中心。也就是说，宇宙对所有地点的观察者都是平权的。这就是“哥白尼原理”，它代表着现代宇宙观的基本精神。

（五）宇宙是静态的，还是动态的？

在发现河外星系的随后若干年，哈勃在几年中对我们周围的许多星系的光谱进行了研究。当星系向远离观测者的方向运动时，每条光谱线的波长都会增加（所谓“谱线红移”）。这就是多普勒效应。由谱线红移的大小可以推算出星系退行的速度。哈勃研究了24个距离已知的星系，从谱线红移发现，它们都远离我们而去，其退行的速度v正比于距离r。（见图15）：

v＝Hr，

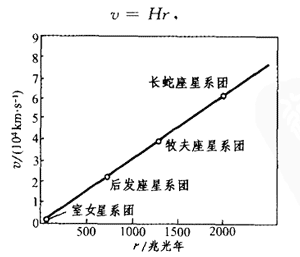
这便是“哈勃定律”，式中比例常量H称为“哈勃常量”，它具有时间倒数的量纲，哈勃定律是1929年发表的，它的深远意义在于向我们展示了一个膨胀的宇宙图像。

1917年爱因斯坦建立了广义相对论，曾试图用来解决宇宙的模型问题。宇宙学原理最早是爱因斯坦提出来的。当时人们对星系和更大规模宇宙结构尚没有什么了解，按照理论物理的习惯，既然对宇宙结构的细节一无所知，就做最简单的假设，认为它是均匀各向同性的。所以宇宙学原理在爱因斯坦那里是一个作业假说。爱因斯坦最初设想的宇宙，是封闭的、有限的和静止的。但是他自己建立的引力场方程却没有这样的解，他在自己的场方程上加了一宇宙项（所谓Λ项），才得到他所想像的静态解。

爱因斯坦引进的Λ常数是要由观测数据来确定的。理论物理学家有一个信条，即能不引进多余的待定常数，就不要引进。可是去掉Λ项，就得不到静态解。这一点不难理解。因为星系间存在着万有引力，只靠引力是达不到平衡的，即使引进Λ项（它相当于某种斥力）。爱因斯坦的静态宇宙模型也是不稳定的。稍受干扰，它就膨胀或坍缩。然而，为什么非找静态解不可呢？要知道，自古以来在人们的观念里，宇宙无始无终，在时间上应是无限的。否则怎样想像字宙创生之前或宇宙末日之后的情景呢？所以人们乐于接受静态的宇宙模型。爱因斯坦也不例外。所以说，在理论上能摒弃这种观念而引入真正的非循环式的动态宇宙模型，应算得上是一种勇敢的设想。

1922年苏联学者弗里德曼（A.A.Fridman）取Λ＝0。得到爱因斯坦原始场方程的非静态解。弗里德曼的理论得到后来发现的哈勃定律的肯定。将弗里德曼的理论与哈勃定律结合起来，可以作出如下推论：存在着一个临界密度ρ_c。

\({\rho _c} = \frac{{3H_0^2}}{{8\pi G}}\)

式中G是万有引力常繁。H₀是当今的哈勃常量，宇宙学中还常用“宇宙学密度”Ω₀的概念：

Ω₀＝\(\frac{{{\rho _0}}}{{{\rho _c}}}\) （ρ₀——当今的密度），

用临界密度或宇宙学密度的概念来表达，则

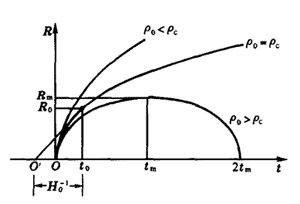
①ρ₀＞ρ_c，Ω₀＞1，宇宙是封闭的，它膨胀到一定时候tm就停止，然后开始收缩；

②ρ₀＜ρ_c，Ω₀＜1，宇宙是开放的，它一直膨胀下去；

③ρ₀＝ρ_c，Ω₀＝1，宇宙处于上述两种情况之间的临界状态。现在我们还不能把哈勃常量确定得很准，比较保险的估计，可取

H₀≈（40～100）km/（s•Mpc），

得ρ₀≈（10^-30～10^-28）g/cm³。

用光度学方法估计宇宙中发光物质的密度为

ρ₀^光度≈10^-31g/cm³＜1%ρ_c，

如果发光物质就是宇宙中的全部物质，则宇宙是开放的，它将永远膨胀下去，然而许多迹象表明，宇宙间还有大量暗物质，其密度尚无法估计，宇宙永远膨胀下去还是将来要收缩，前景未卜。不过当代大爆炸标准宇宙模型中的暴涨理论要求：宇宙处于ρ₀＝ρ_c，Ω₀＝1的临界状态。

前面曾提到，哈勃常量具有时间倒数的量纲，从而H₀^-1具有时间的量纲。从图16可以看出。H₀^-1有个直观的几何意义，是R-t曲线在t＝t₀（现在）时刻切线与t轴交点Oʹ到t₀的距离。该图的坐标原点O代表按上述动力学倒推回去，直到星系与观察者的距离R＝0的时刻，用现代的标准大爆炸宇宙模型（见下文）来解释，O就是宇宙时间的起点，从O到t₀这段时间代表宇宙的年龄T。由于R-t曲线的斜率（即膨胀速度）是递减的，Oʹ必定在O之左，即H₀^-1＞T，故而可以说H₀^-1的物理意义是宇宙年龄的上限。T与H₀^-1之比是宇宙密度Ω₀的函数：

T＝H₀^-1f（Ω₀），

“年龄因子”f（Ω₀）的形式如图17所示，它是随Ω₀的增加而递减的。显然f（0）＝1，且不难证明f（1）＝2/3。

光速c乘以宇宙年龄T，是我们能观测到的宇宙的最大距离；光速c乘以哈勃常量的倒数H₀^-1所得到的长度（称为“哈勃半径”）是它的上限，二者数量级是一样的。所以哈勃常量是一个涉及宇宙时空大小的物理量，其重要意义是可想而知的，然而长期以来它的测量值总是飘忽不定。哈勃原始的测量值是550km/（s•Mpc），由此折算出的宇宙年龄上限H₀^-1≈2.1×10⁹a（年），而从放射性同位素的相对丰度来估算，地球年龄就有4.6×10⁹a，于是产生了“年龄佯谬”。从20世纪50年代到70年代，天文学家一次又一次更精确地校准了“量天尺”，使得哈勃常量的数值一次又一次地减小，达到50km/（s•Mpc）左右，克服了年龄佯谬。然而在以后的20多年里，天文学界的关键人物们一再宣布彼此矛盾的结果，问题始终弥漫在迷雾之中，哈勃空间望远镜的目标是把哈勃常量的数值确定在10%的误差以内，1994年10月宣布对室女星系团中M100星系的12颗造父变星距离的测量结果举世瞩目，因为按测量的距离折算出的哈勃常量H₀^-1＝（80±17.1）km/（s•Mpc），若用标准的大爆炸宇宙模型来推算（Ω₀＝1，T＝2/3H₀），宇宙的年龄只有80亿年左右。可是要和恒星演化理论对球状星团（一种十分年老的恒星集团）年龄的估计相容洽，宇宙的年龄应取T≈（140±20）亿年。于是又一次出现了“年龄危机”。

我们以上讨论的都是宇宙减速膨胀模型，1998年两个独立进行的高红移Ⅰa型超新星巡天的研究小组得到了相同的结论：宇宙正在加速膨胀。要测定宇宙的膨胀速率，必须准确知道退行天体的距离。Ⅰa型超新星是白矮星质量接近钱德拉塞卡极限时产生的爆发现象，它们光度高且比较整齐划一，是天文上比较理想的“标准烛光”。如何理解宇宙加速膨胀这一观测事实？是由于爱因斯坦的宇宙项Λ？是真空能？或是“暗能量”？目前尚无定论。

（六）大爆炸宇宙模型

宇宙在膨胀，今天已是无可怀疑的事实。根据今天宇宙膨胀的速度，可以推算出，宇宙在一二百亿年前脱胎于高温高密状态，开始时膨胀的速度也极大。形象地说，宇宙诞生于一次大爆炸（big bang）。但要注意，所谓“大爆炸’’，并不像一颗炸弹在空中碎裂后弹片四处横飞的那种爆炸。宇宙创生时的大爆炸并不起源于一点，而是整个空间每一点都可看作是膨胀的中心。爆炸过程中每对粒子间的距离都在猛烈地增长，随着宇宙的膨胀，其中的物质密度在减小，温度在下降。

早在1948年，伽莫夫（G.Gamow）和他的同事们就提出了一个“大爆炸”宇宙理论，预言了早期宇宙遗留下一个微波辐射背景，当今的温度应是5K。由于他们的计算在细节上并不完全正确，以及当时高能物理达到的阶段尚不足以使物理学家和天文学家对探索宇宙的早期起源感到有信心，这个理论未受到物理学界的认真对待，在天文学界也鲜为人知。自从20世纪60年代后半期发现3K宇宙背景辐射以来的十年里，情况发生了变化，大爆炸宇宙理论逐渐被广泛接受，以致被天文学家称为宇宙的“标准模型”。谓之“标准”，并非说它在一切细节上都已成熟无误，而是指它已成为检验各种理论思想和论证观测计划的基础。

当今的宇宙中有各种层次的结构，如核子、原子核、原子、分子、地球、太阳系，银河系、超星系团，这都是后来逐渐形成的，早期宇宙的结构却简单得多，其中主要是极高温的辐射和某些种类的粒子在其中自生自灭，好像一锅非常热的羹汤。

宇宙诞生后3分钟，中子和质子全部结合成原子核，这时宇宙中大约有3/4是氢核（质子），1/4是氦核，余下有少量其他轻元素（如锂）的原子核，这是化学元素的原初合成。大约过了三四十万年，原子核俘获了电子，稳定地形成电中性的原子，与背景辐射中的光子脱耦。于是电磁相互作用被屏蔽，长程的万有引力开始起作用，使物质因金斯不稳定性而凝团，逐渐形成星系团、星系、恒星等结构。而脱耦的辐射随着宇宙的膨胀而降温，直到今天留下一个无处不在的3K背景辐射。

在膨胀的宇宙中发生的过程与通常物理实验室里看到的有许多不同。在实验室里闭合系统中热量总是从高温流向低温，温度从不均匀趋向均匀。在膨胀的宇宙中物质与辐射脱耦，由于各自的物态方程不同，温度从相同的初值拉开了，而且差别愈拉愈大。在通常的闭合系统中，密度不均匀的气体总要发生扩散，最后达到均匀的密度。在宇宙中最初密度均匀分布的物质却会在不同的尺度上凝聚成团，在通常的系统中热容量总是正的，这就是说，加热使物体升温，减热使物体降温。然而在宇宙这个自引力系统中热容量是负的，例如恒星晚期热核燃料耗尽时，“炉子”不是冷下来，而是因引力坍缩产生超新星爆发，温度急剧升高。

（七）“热寂说”的终结

1850年克劳修斯建立了热力学，总结出热力学第一定律和第二定律。1854年他进一步引进“熵”的概念，重新表述了热力学第二定律。“热寂说”几乎从热力学第二定律诞生起就是伴随它的阴影，用克劳修斯自己的话说，热力学两条定律意味着：

（1）宇宙的能量是常数；

（2）宇宙的熵趋于一个极大值。

那就是说，全宇宙将达到热平衡，进入热寂（heat death）状态。宇宙热寂的结论固然令人懊恼，但曾经令人困惑的，是为什么现实的宇宙并没有达到热寂状态。长期以来人们认为宇宙基本上是静态，它在时间上无始无终，似乎它早就该处于热寂状态了，由于“热寂说”在感情上和理智上都给人以强烈的冲击，克劳修斯的同时代人就曾群起而攻之，但反对意见多被克劳修斯驳倒了，当时批判“热寂说”的观点中对后世影响较大的有两家之言。

1872年玻尔兹曼提出“涨落说”，我们知道，是他首先赋予了熵增加以统计的解释。按照这种解释，热平衡态总伴随着涨落现象，后者是不遵从热力学第二定律的。玻尔兹曼认为，在宇宙的某些局部可以偶然地出现巨大的涨落，在那里熵没有增加，甚至在减少。这种说法有一定的吸引力，但尚缺乏事实根据。

1875～1876年恩格斯在《自然辩证法》中写道：“运动的不灭不能仅仅从数量上去把握，而且还必须从质量上去理解”，根据这一原则，他有如下的信念：“放射到太空中去的热一定有可能通过某种途径（指明这一途径，将是以后自然科学的课题）转变为另一种运动形式，在这种运动形式中，它能够重新集结和活动起来”。

在苏联和我国以前的一些热学教科书中，除经常引用上面两种说法来批判“热寂说”外，还有过如下一些流行的论点。一种认为宇宙是无限的，不是封闭的，因而不能把热力学第二定律推广到全宇宙。另一种认为，这个问题的答案不可避免地要归到一种“原始推动力”，给“上帝创造世界”的说教以口实。

多少年来，人们总感到对“热寂说”的批判说服力不强，隔靴搔痒，未中要害。现在我们知道了，“热寂说”的要害在于以下两点：一是宇宙在膨胀，二是引力系统乃具有负热容的不稳定系统。我们已看到，由于宇宙在膨胀，它的组分相互会脱耦，从热力学平衡态发展到不平衡态，从温度均匀到产生温差。这种现象在静态宇宙模型中不可能发生，也是克劳修斯和他的批判者们都没有想到的。

此外，金斯不稳定性使密度均匀的宇宙产生了团块结构，形成各种天体。自引力系统是具有负热容的，而具有负热容的系统是不稳定的，它没有平衡态，不能把通常的热力学第二定律用于其上，如果要在这里说到熵，我们欣赏泽尔多维奇（Ya.B.Zel'dovich）提出的看法，对于引力系统，密度均匀态并不是概率最高的。宇宙中均匀物质凝成团块（星系、恒星等）的过程中引力势能转化为动能，从均匀到不均匀，位形空间里的分布概率减少了，但温度上升，速度空间里的分布概率增加了。两者相抵，总概率是增加了，而不是减少了。这就是说，天体的形成是引力系统中的自发过程，它的熵是增加的。由于不存在平衡态，熵没有极大值，它的增加是没有止境的。

总之，膨胀的宇宙和负热容的引力系统以出乎前人意料的方式冰释了“热寂”的疑团，展现了全新的一幅情景：宇宙早期是处于热平衡的高温高密“羹汤”，从这一单调的浑沌状态开始，在膨胀的过程中一步步发展出愈来愈复杂的多样化结构。于是，在微观上形成了原子核、原子、分子（从较简单的无机分子到高级的生物大分子），在宏观上演化出星系团、星系、恒星、太阳系、地球、生命，直至人类这样的智慧生物和愈来愈发达的社会。古埃及神话中的凤凰鸟（phoenix）焚身于裂火之后，从自己的灰烬中青春焕发地再生，这是当代宇宙观的一幅精彩写照。宇宙不但不会死，反而从早期的“热寂”状态（热平衡态）下生机勃勃地复生，固然，当今的宇宙学尚不能准确地预卜宇宙的结局，但是折磨了物理学界和哲学界100多年的梦魇——热寂说，作为历史的一页，可以尽管放心地翻过去了。

发布时间：2013/12/31 下午3:08:10  阅读次数：10740