第三章C 牛顿定律的应用教学建议

（一）学习目标

1．理解牛顿第一、第三定律。掌握牛顿第二定律，能综合运用牛顿运动定律和运动学公式解决一些简单的实际问题。

2．通过已知力求运动，已知运动求力的两种最基本解题过程，认识建模、分析、综合等科学方法在解决简单的实际问题中的作用。

3．通过牛顿定律的解题训练，感悟动力学和运动学知识在交通、宇航等实际应用中的重要作用，从而加强学习的自觉性和使命感。

（二）重点和难点

本节的重点是在两类基本问题中综合运用牛顿定律和运动学公式解题，本节的难点是在实际问题中进行建模和受力分析、过程分析。

（三）教学建议

本节教材的牛顿定律应用与基础型课程中的有关应用相比，应当说综合性更强，要求更高，对有关念、规律的运用更全面、更熟练，并且与生活、技术的联系也更加紧密。

本节从航天飞机着陆事例引入问题，接着指出两类典型问题，以及它们在科学与技术中的重要意义，再通过一个竖直方向的运动实例和一个水平方向的运动实例分析，说明解决这两类典型问题的基本方法。接着对学有余力的学生又介绍了连接体问题，说明牛顿运动定律不仅适合于单个物体，也适用于多个物体组成的系统，或一个物体中的某一局部。最后还介绍了物理学中常用的估算方法，即运用近似方法对实际比较复杂的物体进行简化后，运用物理规律解决问题的方法。

通过本节学习使学生对牛顿定律无论从认知水平、思想方法还是应用能力诸方面能提升到一个新的高度。

本节建议安排3课时，第1课时学习示例1、示例2，并随堂做一些练习部分的问题。

第2课时学习示例3及练习部分的示例。第3课时学习连接体问题和估算方法，也可以继续学习示例或讨论较难的练习题。

1．关于引入部分的说明

本节引入部分从交通工具入手是因为它们比较具体、直观，而且这类运动比较接近匀变速运动。航天飞机拖着减速伞滑行时，可根据跑道长度求阻力，也可已知阻力求跑道长度，包含了两类基本问题。类似的还有舰载飞机从航空母舰上起飞与降落问题。

2．关于两类典型问题的教学建议

由于基础型课程中已经提到过两种典型问题，本节教学可先回顾这两种情况，要求学生通过“大家谈”联系实际问题谈这两种类型。如发生车祸时可根据轮胎在路面上擦出的摩擦痕迹长度推知车辆的初速度是否超速（v₀＝ $\sqrt{2 μ g s}$ ）。运动员踢一个静止足球时可根据踢出时的球速、触球的时间与球的质量，估算出他对球的平均作用力（ $\bar{F} = \frac{m v}{t}$ ）等。

教材中把两种基本类型问题推广至火箭、飞船、粒子加速器以及发现定律、规律上，借以扩大学生的视野，懂得牛顿运动定律的应用价值。

3．关于课本第35、36页示例的教学建议

示例1中子弹运动时除了受到5000N推力之外，还受到枪管的阻力，显然这个阻力与5000N推力相比要小得多，在这里作了理想化处理，忽略不计了。

示例2中也有许多理想化处理，如将人看作质点，夹紧的力看作集中在腿上，有两个压力，因而产生两个摩擦力。

本题“讨论”中说用570N的力夹管子求着地速度，实际上已变成了已知力求运动那一类问题了。这时2个摩擦力产生的合力为2F_f＝2μF_N＝2×0.4×570N＝456N，仍小于重力600N，故消防员下落做匀加速运动，则a＝ $\frac{600 - 450}{60}$ m/s²＝2.4m/s²，于是求得v_t＝ $\sqrt{2 a s}$ ＝ $\sqrt{2 \times 2.4 \times 7}$ m/s＝5.8m/s。

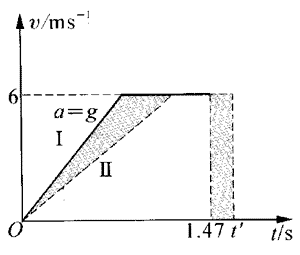
本部分的“拓展联想”中自由下落的时间 $t_{1} = \frac{v}{g} = \frac{6}{10} s = 0.6 s$ ，后面匀速运动的时间 $t_{2} = \frac{7 - \frac{1}{2} \times 10 \times {0.6}^{2}}{6} s = 0.87 s$ ，所以下落的总时间是1.47s，比示例中下落时间 $t = \frac{s}{\bar{v}} = \frac{7}{3} s = 2.3 s$ 要少得多。从图3-7中的图象可以看出，先自由下落后匀速（图线Ⅰ）比其他方案（图线Ⅱ）下降的时间都短（图中阴影部分面积相等），因此这种方案是最快下降的方案。

示例3是已知力求运动的问题，难在有前后2个过程，受力情况发生了变化，教学时可提出一系列问题让学生思考，如：

（1）本问题属于哪一类问题？有哪几个过程？

（2）前一过程受力如何？加速度为多大？

（3）后一过程受力如何？加速度为多大？

（4）前后两过程有怎样的联系？

分析讨论之后再着手解题，也可采用教师引导下边讲边练的形式进行，效果可能会更好。

应当向学生指出题目没有固定的所谓类型，也不要过分拘泥于解题类型划分，有些题可能兼有两种类型，有些题可能是已知力和运动求物体的质量等等。

4．关于连接体问题的教学建议

本部分教学的关键是用隔离法进行受力分析，分析时应标好每一个力的符号，特别是作用力与反作用力的符号。

课本第38页“大家谈”中设木块质量m_B＞m_A，F相同，所以无论向右还是向左推木块，加速度a是相同的。向右推时设相互作用力为F_AB，则F_AB＝m_Ba；向左推时，设相互作用力为F_BA，F_BA＝m_Aa，由于m_B＞m_A，因此F_AB＞F_BA。即向右推时木块间相互作用力大于向左推时木块间相互作用力。

课本第38页“自主活动”中当两物体有共同加速度时，可以将两者看成整体，先求出加速度，即 $a = \frac{F - F_{f 1} - F_{f 2}}{m_{1} + m_{2}}$ ＝1.96m/s²，然后用隔离法求出F_T，F_T＝m₂a＋F_f2＝5390N。

5．关于估算方法及相关示例的说明

本题涉及到的是一种数量级的估算。“学习物理就应该经常练习对事物作粗略的数量级估计，留心尺度大小改变时所产生的影响，有意识地将这种做法养成习惯，久而久之，可以加深我们对物理现象的实感，从而增进我们对事物本质的洞察能力。”（赵凯华：《定性与半定量物理学》）。这段话也就是教材编入这部分内容的主要意图。供学有余力的学生选读。

常用的估算方法大致是：

1．直接记住一些基本常数或经验常识中某些物理量的数量级，作为估算的出发点；

2．寻求量与量之间的关联，通过比较、类比进行估计；

3．从基本原理出发通过建模和近似方法来估算。

例如：试估算人在空气中受到的浮力是人自重力的10^-1，10^-2，10^-3还是10^-4。

浮力的大小F_浮＝ρ_空gV_排，重力的大小F_重＝ρ_人gV_排，V_排是相同的，所以F_浮/F_重＝ρ_空/ρ_人。由于人的密度接近于水的密度，即ρ_人≈ρ_水＝1.0×10³kg/m³，ρ_空＝1.29kg/m³，所以是F_浮/F_重 ≈10^-3。本题主要运用的是估算方法的前两种，教材中的示例，运用的是第3种。

（四）作业说明

练习部分共有17道题，建议第1课时完成A组第1至第6题，B组第10题；第2课时完成A组第7至第9题，B组第11至第12题；第3课时完成B组其余各题。

参考答案

A组

1．ABC

2．D

3． $\frac{2 M a}{g - a}$

4．如图

图3-8

5．20N

6．C

7．CD

8．D

9．（1）120N（2）13.5m

B组

10．A

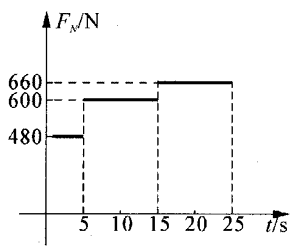
11．（1）600N（2）2400N（3）57kg

12．480m，11250N（设没有空气阻力）

13．（1）3000m（2）2.152倍

14．1/150

15．（1）1.5×10⁴N（2）7.5×10³N（3）1000m

16．0.5

17．（1）开始做变加速运动，最后做匀速运动（2）2.45m/s²，0（3）当t＝0时，mgsinθ－μmgcosθ－kv₀＝ma₁；当v₂＝10m/s时，mgsinθ－μmgcosθ－kv₂＝0，解得 $k = \frac{m a_{1}}{v_{2} - v_{0}}$ ＝1.96，动摩擦因数μ＝0.75

文件下载（已下载 177 次）

发布时间：2013/12/25 上午7:49:26 阅读次数：1803