第二讲B 动能定理的应用教学建议

（一）学习目标

1．掌握动能定理，应用动能定理解决一些简单的实际问题。

2．在应用动能定理的过程中能运用抽象、建模、分析、综合等科学方法。

3．通过动能定理的实际应用感悟动能定理在技术和社会中的重要应用价值。

（二）重点和难点

本节的重点是动能定理的应用，难点是多过程和变力做功情况下动能定理的应用。

（三）教学建议

本节从一辆轿车以恒定功率做变加速运动的实际事例中引出问题，为提出用牛顿定律难以解决的情况下用动能定理能否解决问题创设了情景，接着指出了解题步骤方面的几个要求。通过示例1说明动能定理能在曲线运动中加以运用，示例2说明动能定理在物体受力有先后的“多过程”中的应用，最后在示例3中又回到本节开头所创设的情景中变力做功情况下动能定理的应用。通过本节不但指明了运用动能定理的解题规律，还表明了动能定理在解决某一类问题时，有它的特殊的优越性。

本节与练习题中共有五道例题，可用2课时来完成。

1．关于示例1的教学建议

本示例编写时注意到与课本23页中提出的4条注意点密切配合，使学生对解题步骤有一个确切的体会。应当指出这里所用的表达式是“代数和”表达式，而不是“合力功”表达式。因为这里小球受到的合力足一个变力，难以进行计算。

2．关于示例2的教学建议

本示例结合图象运用“代数和”表达式解题，要求与牛顿定律解法作对照，进一步表明动能定理的优越性，用牛顿定律结合运动学公式的解法如下：

设第1过程加速度为a₁，末速度为v₁；第2过程加速度为a₂，末速度为v₂；第3过程加速度为a₃，末速度为v₃，则

$\begin{array}{l}{a}_1=\frac{F_1}{m}=1m/s^2,v_1=\sqrt{v_0^2+2a_1{s}_1}=\sqrt{9+2\times 1\times 2}m/s=\sqrt{13}m/s\approx 3.6m/s\\ a_2=\frac{F_2}{m}=2m/s^2,v_2=\sqrt{v_1^2+2a_2{s}_2}=\sqrt{13+2\times 2\times (6-2)}m/s=\sqrt{29}m/s\approx 5.4m/s\\ a_3=\frac{F_3}{m}=-1.5m/s^2,v_3=\sqrt{v_2^2-2a_3{s}_3}=\sqrt{29-2\times 1.5\times 2}m/s=\sqrt{23}m/s\approx 4.8m/s\end{array}$

所得的结果与示例2相同，但显得繁琐得多。

3．关于示例3的教学建议

本示例与练习部分的示例2都涉及到用机械的功率保持不变这样一个条件来解题，由于P＝Fv，式中P不变，v增大，则F一定减小，属于变力做功。但根据W＝Pt，力做的功却是随时间均匀增加的。只要知道做功的时间，就能求出牵引力所做的功。

对这类问题通常要用好两幅图象，图1表明牵引力随时间变化的情况，起步不久速度小，牵引力可以较大。当速度增大后牵引力应当减小，但车辆仍然在加速，最终当牵引力等于阻力时加速度变为零，车辆维持匀速运动，图2表明牵引力所做的功随时间变化的情况，功与时间成正比，图线的斜率就是功率P，保持不变。

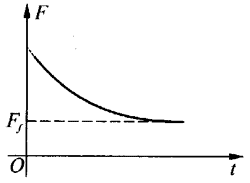
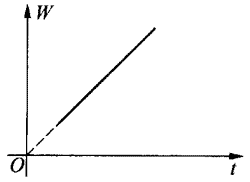
图线的虚线部分表示不研究车辆刚起步的情况。机械不可能始终保持功率恒定的状态，起步时v＝0，F不可能是无限大。

（四）作业说明

本节共有13道练习题，第1、4、8题建议在课内完成，第1课时可完成第2、3、5、6、7、9各题，第2课时完成其余各题。

参考答案

A组

1．AD

2．2.5×10⁹

3．每秒钟动能的变化量即电功率，ΔE_k＝$\frac{1}{2}$ρSv²＝5200W

4．BD

5． $\frac{\sqrt{3}}{6}$v₀

6．1000W

7．初状态是动能为零的开始状态，末状态是m₁刚抛出时的状态，要测定的物理量是m₁、m₂、h、μ、m₂及落地时水平位移s和滑轮离地面的高度H，计算式是$m_{2}gh-\mu m_{1}gh=\frac{1}{2}(m_1+m_2)\frac{s^{2}g}{2H}$，即$s=\sqrt{\frac{4hH(m_2-\mu m_1)}{m_1+m_2}}$

B组

8．D

9．C

10．112.5

11．$\frac{5}{12}$Fh

12．μ＝tanθ

13．（1）1000N（2）2.9×10⁵J，1475N（3）14.75s（4）0.38m/s²

14．$\frac{mg(H+26h)}{60\eta }$

15．2.58×10⁸W

发布时间：2013/11/29 上午7:51:48  阅读次数：1665