利用匀速圆周运动测运动物体的速度

江西都昌县第一中学 李一新 选自《物理教师》2012年第9期

匀速圆周运动是常见运动模型中的一种。利用此运动可测出一些运动物体的速度。

1．测子弹的速度

1.1 旋转圆筒法

让子弹穿过匀速旋转的圆筒，由于子弹的速度很大，可看成是匀速直线运动，在匀速旋转的圆筒上留下子弹穿过的孔，通过匀速圆周运动的知识求出子弹穿过圆筒的时间，从而可测出子弹的运动速度。

（1）一孔法

【例1】如图1所示，直径为d的圆筒绕中心轴作匀速圆周运动，角速度为ω，枪口发射的子弹沿直径匀速穿过圆筒。若子弹穿出后在圆筒上只留下一个弹孔，则子弹运动的速度可能为多少？

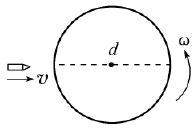
【解析】子弹穿过圆筒后作匀速直线运动，当它再次到达圆筒壁时，若原来的弹孔也恰好转到此处，则在圆筒上只留下一个弹孔。所需的时间为\(t = nT + \frac{T}{2} = \frac{{2\pi }}{\omega } \times (n + \frac{1}{2})\)，其中n＝1，2，3……，则子弹的可能的速度为\(v = \frac{d}{t} = \frac{{d\omega }}{{\pi (2n + 1)}}\)，其中n＝1，2，3……。

（2）两孔法

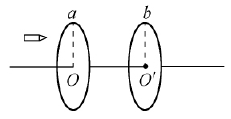
【例2】如图2所示，直径为d的纸质圆筒以角速度ω绕轴匀速转动，枪口对准圆筒上a点沿直径方向发射一颗子弹，在圆筒旋转不到半圈的时间内，子弹恰好从b点穿出。已知aO和bO之间的夹角为θ，则子弹的速度v是多少？

【解析】根据题意可知，圆筒不转，子弹将直接打在aʹ上。圆筒转动，子弹打在b点上，则子弹在圆筒内运动的时间等于圆筒转过（π－θ）角所用的时间，所以子弹的速度为

\(v = \frac{d}{t} = \frac{d}{{\frac{{\pi - \theta }}{\omega }}} = \frac{{d\omega }}{{\pi - \theta }}\) 。

【点评】上述两方法是利用子弹的匀速直线运动和圆筒的匀速圆周运动相结合来测量的。通过匀速圆周运动计算时间。缺点是子弹在圆筒中实际是作平抛运动。

1.2 旋转双圆盘法

让子弹水平穿过两个间隔一定距离的同轴转动的圆盘，子弹在水平方向作匀速直线运动。根据穿过两圆盘孔的角度，利用匀速圆周运动的知识求出时间，从而可测出子弹的运动速度。

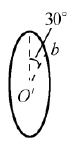
【例3】为了测定子弹射出枪膛时速度，在一根水平放置的轴杆上固定着两个薄圆盘a、b，a、b平行相距2m，轴杆的转速为3600r/min，子弹穿过两盘留下两个弹孔c、d，测得两孔所在的半径间的夹角为30°，如图4所示，则该子弹出膛速度v是多少？

【解析】如图3所示，在子弹击穿薄圆盘a时刻，子弹、圆盘的a点和b点均在同一竖直平面内，子弹在圆盘a和圆盘b之间飞行时，圆盘a、圆盘b均在匀速转动，当子弹击穿圆盘b时bOʹ已转到了图4的位置，则子弹在圆盘a和圆盘b之间的飞行时间等于圆盘b转动30°角所用的时间，故子弹的速度为

\(v = \frac{{\overline {OO'} }}{t} = \frac{{\overline {OO'} }}{{\frac{\pi }{{6\omega }}}} = \frac{{\overline {OO'} }}{{\frac{\pi }{{12\pi n}}}} = 12n\overline {OO'} = 1440m/s\)

【点评】此方法是利用子弹的平抛运动和圆盘的匀速转动相结合来测量的。克服了旋转圆筒法子弹在圆筒中作平抛运动的缺点。

2．测汽车的速度

汽车行驶时，车轮边缘的线速度即为行驶速度，因此只要测出汽车车轮的转速和半径就能测出汽车行驶的速度。

【例4】如图5所示，表示一实验小车中利用光电脉冲来测量车速和行程的装置。A为光源，B为光电接收器，A、B均固定在车身上，C为小车的车轮，D为与C同轴相连的齿轮，车轮转动时，A发出的光束通过旋转齿轮上齿的间隙后变成脉冲光信号，被B接收并转换成电信号，由电子电路记录并显示。若实验显示单位时间内的脉冲数为n，累计显示的总脉冲数为N，则要测出小车的速度和行程还必须测量的物理量或数据是__________；小车速度的表达式为_________；行程的表达式为________。

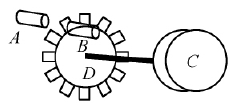
【解析】设小车车轮的转速为n₀，车轮的半径为R，则小车的速度为v＝ωR＝2πn₀R。设齿轮D的齿数为P，因D转一圈即转过P个齿，单位时间内的脉冲数n即为单位时间内转过的总齿数，因此单位时间内的转数\({n_0} = \frac{n}{P}\)，从而得小车的速度表达式为

\(v = 2\pi {n_0}R = \frac{{2\pi nR}}{P}\)

可见，必须测量的物理量或数据是车轮的半径R，齿轮D的齿数P。

（2）累计显示的总脉冲数为N时经过时间为\(t = \frac{N}{n}\)，因此行程的表达式为

\(x = vt = \frac{{2\pi nR}}{P} \cdot \frac{N}{n} = \frac{{2\pi NR}}{P}\)

【点评】本题中关于转速的测定是通过测定齿轮的总齿数和单位时间内转过的齿数来进行。

3．测雾滴的速度

雾滴的速度一般不易测量，利用匀速圆周运动可同时解决运动的距离和时间，从而可测出某种雾滴的速度。

【例5】利用如图6所示装置可以测定油漆喷枪喷射油漆雾滴的速度。

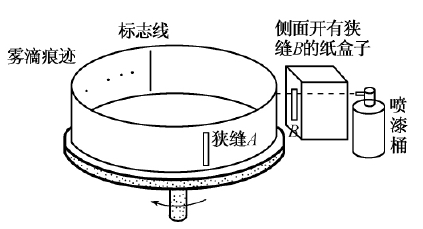
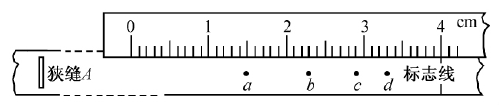
（1）将直径D＝40cm的纸带环，安放在一个可以匀速转动的转台上，纸带上有一狭缝A，A的正对面有一条标志线。油漆喷枪放在开有狭缝B的纸盒里。转台以角速度ω＝2.1rad/s稳定转动后，开始喷漆。仅当狭缝A和B正对平行时，雾滴才能在纸带内侧留下痕迹。改变喷射速度重复实验，在纸带上留下了一系列的痕迹a、b、c、d。将纸带取下放在刻度尺下，如图7所示。已知v₀≥\(\frac{{\omega D}}{\pi }\)，则速度最大的雾滴所留的痕迹应为_________点，该点离标志线的距离为__________cm，该喷枪喷出的雾滴的最大速度为_________m/s，若考虑空气阻力的影响，该测量值______真实值（选填“大于”“小于”或“等于”）。

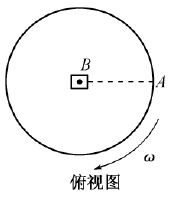
（2）若将喷枪和开有狭缝的纸盒置于转台上，如图8所示。喷枪固定于转轴上不随台转动，而纸盒随转台转动，且使狭缝A和狭缝B始终正对。开动转台，转台以角速度ω稳定转动。改变喷射速度，重复实验4次。（已知v₀≥\(\frac{{\omega D}}{\pi }\)）则

（A）喷枪喷出液滴一定不会从狭缝A射出

（B）喷枪喷出液滴可能会从狭缝A射出

（C）只要时间足够长，纸带上将到处留下液滴的痕迹

（D）速度越快的液滴在纸带上留下的痕迹离狭缝A越远。

【解析】（1）油漆雾滴通过狭缝A后可看作匀速运动，打到纸带的时间为

\(t = \frac{D}{{{v_0}}}\) （1）

与此同时，纸带环随转台转过一个角度，通过一段弧长Δl，由于v₀≥\(\frac{{\omega D}}{\pi }\)，油漆雾滴射到纸带环上的时间\({t_0} = \frac{D}{{{v_0}}} \le \frac{\pi }{\omega } = \frac{T}{2}\)，弧长不会超过半个圆周，则所需的时间为

\(t = \frac{{\Delta l}}{{\omega \cdot \frac{D}{2}}} = \frac{{2\Delta l}}{{\omega D}}\) （2）

由（1）、（2）两式得油漆雾滴的速度为

\({v_0} = \frac{{\omega {D^2}}}{{2\Delta l}}\)

可见，通过的弧长越小，油漆雾滴的速度越大。所以，速度最大的雾滴所留的痕迹应为d点，该点离标志线的距离为7.0cm，代入数据得雾滴的速度最大值为24m/s，由于空气阻力的影响，该测量值小于真实值。

（2）由于v₀≥\(\frac{{\omega D}}{\pi }\)，油漆液滴射到纸带环上的时间\({t_0} = \frac{D}{{2{v_0}}} \le \frac{\pi }{{2\omega }} = \frac{T}{4}\)，故喷枪喷出液滴不可能从狭缝A射出。速度越快，射到纸带环上的时间越短，纸带环转过的角度越小，在纸带上留下的痕迹离狭缝A越近。故正确选项为（A）。

【点评】匀速圆周运动转过一定角度的时间，一般很难测出，本题中通过纸带测出弧长，能方便地测出运动的时间。

发布时间：2013/10/22 上午11:27:56  阅读次数：6969