谁会下滑得更快些
在滑雪的好季节里，一位读者向我们提出了一个他百思不得其解的有趣问题，希望我们能帮助他明白其中的奥妙。他说："我注意到一个现象：我是一个体重为95公斤的人，与其他朋友一块儿在一个倾斜度相同的山坡上滑雪。当我开始自由下滑时，一位比我矮小的朋友也同时向下自由滑行。开始时，我比他落后4～5米，但后来我滑得越来越快，不但弥补了差距，而且还超过了我的朋友，将他远远地抛在了后面。这是为什么呢？在学校里学到的物理知识告诉我们，重力是以同样的方式作用于所有物体的。"换句话说，这位读者的意思是：为什么体重越大下滑的速度越快？尽管他在开始时并不那么快。
这个问题实际上并不像人们想像的那么简单，因为作用于滑雪者的力，除了重力之外还有另外一些不同的力。在这些力中，首先是空气的阻力，它的大小取决于速度；然后有雪地的摩擦力，它则取决于滑雪者的体重和滑雪的速度。就像伽利略所做的那样，让我们来具体地分析一下滑雪的机理（暂且不考虑一些小的效应），并根据影响滑雪者的各种因素的重要性的不同而做出不同的解答。我们将应用几乎是不可缺少的最低限度的一部分公式来说明问题。如果理解公式有困难的话，也可以不去管这些公式，只要认真读一下有关的文字解释就可以了。
初始速度近似相同
让我们先来分析两个滑雪者是以相同的速度下滑这一情况。正如在学校里学过的，重力加速度对所有的物体都是一样的。但这种理论却同读者在现实生活中仔细观察到的情况相矛盾。如果我们要演示一下上述情况的可能性，就需要把空气的阻力排除在外。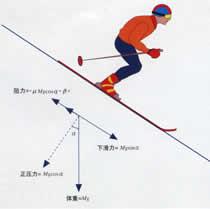
让我们先来具体地考虑一下作用于滑雪者的各种力（见图1）。如果我们以M表示滑雪者的质量，g表示重力加速度，α表示下滑斜面的倾角，那么这些力就是：
1．体重下滑分力。它的方向与下滑平面平行，是由Mg乘以倾角α的正弦得出的；
2．雪的摩擦力。它与动摩擦系数（这里以μ来表示）有关，显然还与滑雪者向雪表面施加的正压力成正比，这种压力就是垂直于下滑平面的体重分力（Mg乘以倾角α的余弦）；
3．空气的阻力。在一般的况下，它与速度v成正比，并与β系数有关，β系数是既考虑到了空气的黏度，也考虑了滑雪者的空气动力学因素。
那么要描述运动，或者找到加速度（以a来表示）就只有写出牛顿定律，根据这一定律，阻力是以负号来表示的：
Mgsinα―μMgcosα―βv = Ma
（下滑作用力＋雪的摩擦力＋空气阻力＝质量乘以加速度）。在写出的等式中可以看到，如果βv ≈ 0，或者说，如果空气阻力这一项可以排除，那么运动员的体重就可以抵销。在此情况下，也只有在这种情况下，加速度就是：a＝g (sinα-μcosα)
很明显，这对所有滑雪者都是相同的，因为滑雪者的加速度只取决于倾斜度、重力加速度和摩擦系数，而与体重无关。
用数字举例说明：倾斜度α=20°，动摩擦系数μ=0.1，那么a＝9．8×（0.324-0.094）=2.43m／s2，这种情况只是在开始时很短的一段时间内才近似正确，也就是在速度还很小和空气阻力无足轻重的时候。除此之外，两个人所具有的其他条件也要完全相同，比如滑雪板的滑动性能要一样（即μ完全相同）。
体重轻滑得慢
有没有一种办法使体轻的话也能取胜呢？让我们把阻力的因素考虑进去看看会有什么结果。伽利略已经就重物下落的问题进行过讨论。他观察到（为了简明易懂，这里仅涉及一个球体）：作用力即重量的增长，是像体积一样增长，或者说是立方的形式增长；而空气动力的阻力的增长则像平面一样增长，或者说是以平方的形式增长。这就使人们可以说空气阻力是按照平方量的立方根的形式增长（也就是说β＝γM 2/3，在这里γ是一个常数）。代入上述的牛顿定律的等式中，并将各项除以M，就成了：
a = g(sinα-μcosα)-γν/M 1/3
很显然，将空气摩擦因素考虑进来对体重轻的滑雪者是不利的。因为在速度相同的情况下，体重越轻，加速度也就越小（带入数字可知：当滑雪的体重从95公斤减到65公斤时，等式中的减速项γM 1/3增加了13％）。
以体重取胜
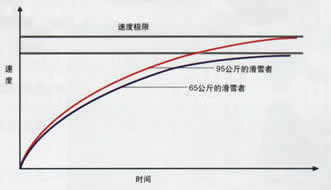肥胖的滑雪者应滑得更快一些，这好像不成为问题。为了确认这一点，让我们计算一下终速状态，也就是当随着速度增大而增加的空气阻力加上雪摩擦力与下滑力相等的时候达到的那种状态。在此限度内，牛顿定律的等式中的加速度就变成了0；取一个γ的合理值0.24kg1/3s，就可得出可以达到的最大的时速：95公斤体重的滑雪者为166公里/小时，而65公斤体重的滑雪者则为147公里/小时，后者只有在自己身上压上铅块（但愿他的双腿能够承受得了）或许能够战胜他的朋友。在图2中显示出按时间标出的两位滑雪者速度变化情况的坐标。
雪的润滑作用
上述一切是一种非常微妙的设想，也就是假设雪的摩擦系数μ对各种滑雪者来说都是一样的，而不考虑他的体重和滑雪板与雪之间的接触状况。与其他的滑行面相比，在雪上滑行的摩擦力较小，因为摩擦本身能产生热量，热能够融化了一部分雪，从而在滑雪板的底板上形成一层薄薄的润滑层（如果地面是玻璃碎屑，那就不可能滑动了）。滑雪时在单位时间内产生的热量与速度和摩擦力有关：在速度相同的情况下，较肥胖的滑雪者比体重较轻的滑雪者能使滑雪板与雪之间产生更多的热量，能更快地消融雪，从而使其μ系数必然变得更小。
如果情况的确如此的话，那么雪融的效能减低就能使μ系数重新增大……不过，滑雪的过程实际上极其复杂，影响因素很多，想用精确的数量来表述它并非易事，因此很难准确地解释清楚我们的读者朋友提出的问题。比如，在他们出发时我们计算的是静摩擦系数，它与动摩擦系数有很大的区别；而现在谈到的情况更为特别，要产生热量就必须运动。在整个低速运动阶段，由于空气阻力尚未占主导地位，热量的产生可能仍然与需求不相适应，从而使滑雪板底板的各种不同的性能显得十分重要。
总之，每一位读者都可以发表自己的意见和看法。首先是如果有机会去滑雪的话，一定要同自己的伙伴一起做个比较精确的实验，然后在可能的情况下，将每一个有趣的结果告诉我们。
发布时间：2007/5/24 下午4:30:28 阅读次数：11992
