地球半径巧测量

两千多年前，哲学家们找到了测量地球半径的方法，只需量一下影子的长度就可以 计算出地球的半径。不知读者朋友们能否在一间邻海的房子里只借助一只表和一把皮尺测量地球半径呢？

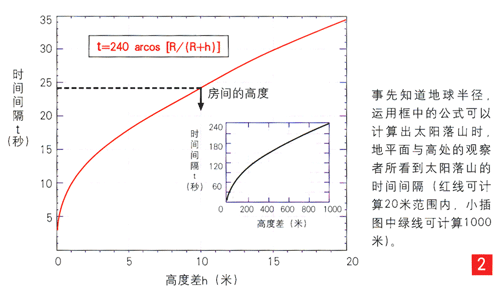
假如你正在海边度假，住在一家临海旅馆四层的一个房间里，房间视野很开阔。有一个人悬赏说，明天天亮以前，谁要能想出一个相当准确的方法来测量地球半径，将获得一笔奖金，条件是除了借助一只表和一把皮尺外，不能使用特别的仪器。你能做到吗？

先别急着往下看，也不要看图，你先仔细想一想。你就想象你在旅馆里，房间的位置如上所述，免得你走弯路。

答案

你可以测一下房间的窗台离地面有多高，当然也可以问旅馆老板：我们假设为10米。黄昏时分，你趴在旅馆前的海滩上，请你的朋友坐在你房间里把下巴倚在窗台上。为了不使问题过于复杂化，我们可以这样设想，趴着时你的眼睛处在地平面上。当太阳的上边或者说最后一个亮点消失在海平面上时，你按下秒表开始记时。此时，从你朋友那里看，太阳还有一点仍处在海平面上，当太阳消失的一瞬间，让你的朋友喊声“停！”，你就让秒表停下。你可能会觉得奇怪，不过这中间确实要经过24秒多（准确的结果应该是24.366秒）。

现在，你需要一点三角函数知识来推导出地球的半径。如图1所示。对于趴在海滩上的人来说，太阳的上边没入海平面时，太阳发出的光线与地球相切于他趴着的地方，如图上线段AB所示。处在高处的人看到太阳落山时的最后一缕光线，与地球相切的那条线是线段CE。设高处的观察者所在的高度为h，地球的半径为R。三角形ODE是直角三角形。根据余弦定理，直边OD＝R与斜边OE＝R＋h的关系式为R＝（R＋h）cosθ，其中cosθ是θ角的余弦。另外，我们知道，地球转过这个θ角需要24.366秒（如果不出偏差）；因为转一周要用24小时，这样可以得出：θ／360＝24.366／（24×3600），结果θ＝0.101525°。用一个小计算器可以算出θ的余弦等于0.99999843；代入上面的三角公式，其中h＝10米，这样得出R≈6370公里，正好是地球半径。不用三角函数知识，也可以计算出同样的结果，只不过需要比较复杂的几何推理。

站直了和趴下

当然，事情不可能像描述得那么理想，会有各种误差。比如，你的眼睛不可能恰好处在地面上，而且你找的人头脑反应快慢的问题等等，这样得到的数据可能会有5％左右的偏差。如果你的房间在11层，或者最好你的朋友在海边一个巨大的峭壁上，而你在峭壁的底部，通过手机接收他发出的停止指令，这样偏差就会小些。在意大利的拉齐奥（Lazio）就有一个好去处：在海边有一座高600米的山，从高处到水平面大约有3分钟的延迟，偏差几乎为零。如果没有人帮忙，你可以自己试一下，沿着台阶跑上去，但愿时间来得及。你还可以通过测量你趴在地上和站直身体时看到太阳落山的时间问隔进行计算。既然上面用到的几何关系式表明间隔与两个观察点的高度差成正比，那么如果你站直身体时眼睛的高度为1.70米，时间间隔就应该是10秒，不同的是高度差太小，时间太短而已（图2）。令人感到意外的是，虽然古人知道地球是圆的，而且早在公元前，毕达哥拉斯和亚里士多德就明确地指出这一点，但据我们所知，古人从来没有用过这么简单的方法来估算地球的半径。这其中的原因也许是那个时代人们很难准确地测量时间。

井中的太阳

历史上第一个做此种尝试的是希腊天文学家埃拉托斯特尼（Eratosthenes，公元前280～前190年），他的试验比较复杂。埃拉托斯特尼认为，在赛伊尼（Syene），即位于今天的亚历山大以南的阿斯旺（Assuan），在夏至日的正午，太阳差不多经过天顶：他知道窄窄的井底被照亮。而在亚历山大，情况就不一样了，影子不可能消失，即太阳总是斜射的。他观察了日晷指针（或一根竿子）的影子，而且他还知道太阳射到地球上的光线是平行的，通过计算影了和指针的长度关系，他得出结论：正午时分，在亚历山大，太阳光会与地面的垂直线有一个7.2°的夹角，相当于地球圆周角的1／50（图3）。

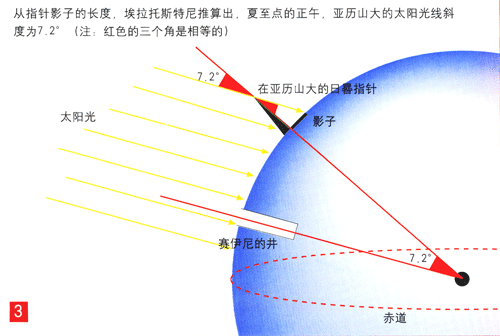
如图所示，因为这个角度与赛伊尼和亚历山大之间的经线弧度相等，于是只需确定这段距离的长度，再乘以50即可。然而在当时，测量这两地之间的距离也非易事。

根据一个驼队走完这段距离半均所花的时间，埃拉托斯特尼得出这段弧长为5000斯塔迪亚（1斯塔迪亚约为178米），那么经圈的周长为5000×50＝250000斯塔迪亚，得出半径长为7080公里，大约多出10％。不过，能根据骆驼的脚程计算出这样一个数来已经不错了。

公元前1世纪，希腊哲学家波塞多尼奥斯（Poseidonius）做了进一步努力：这是第一次利用天文方法进行测量，得出的值比埃拉托斯特尼的数值略低。波塞多尼奥斯利用的是洛迪（Rodi）和亚历山大之间的经线，他根据船航行两地用的平均时间，井且根据老人星（Canopus）在同一时刻处在两座城市上的不同位置确定中心角。事实上，这颗星在洛迪处在地平线上时，它的光线则以7.5°的斜角照到亚历山大。在事隔900年后，阿拉伯人开始尝试再一次测量地球半径。他们也是在天文观测的基础进行的，不过任务更艰巨。他们在地上，准确地说就在巴格达附近的平原上，选取了两个参照点竖起木竿。他们得到的结果更加精确，只有3.6％的误差。

你也来试试

最后，建议读者朋友们按照上面的方法试一试，并把结果告诉我。可能的话，我建议大家去靠海的天然高地，时间就选在黄昏时分。

发布时间：2007/4/16 下午3:25:05  阅读次数：26800