第四章 B 角速度与线速度的关系

执教：上外附属大境中学 方成亚

一、教学任务分析

本设计的主要内容有：角速度，角速度与线速度的关系，角速度、线速度与周期及转速的关系。它是对描述匀速圆周运动的进一步学习，也是今后学习“向心力、向心加速度”等内容的重要基础。

本课从观看教室中电风扇的转动入手，通过对叶片上各质点运动相同点、不同点的比较，建立角速度概念。

通过实例首先让学生讨论角速度与线速度的关系，进而利用已学物理学知识、数学知识推导它们的关系，以达到对知识的真正理解，起到突出重点，突破难点的作用。

教学中通过对自行车等实际物体运动的探索研究，让学生感受到圆周运动在生产、生活、科技中的广泛存在及应用，从而对圆周运动问题产生较强的兴趣，也为以后的学习打下较好地基础。

二、教学目标

1．知识与技能

（1）理解角速度的概念并知道其单位。

（2）理解角速度与线速度的关系。

（3）知道周期、转速与角速度、线速度的关系。

2．过程与方法

（1）通过从实例的分析建立“角速度”概念的过程，认识到联系实际进行分析、归纳是建立物理概念的重要方法之一。

（2）通过应用比较的方法，认识描述“直线运动”和“圆周运动”方法的区别，感受比较的方法在区分类似物理概念中的作用。

3．情感、态度与价值观

（1）通过对生活实例的分析以及对自行车相关问题的探索研究，感悟物理源于生活，提高学习物理的兴趣。

（2）通过教学过程中的讨论、交流，感受交流合作是学习的重要方式之一，激发与他人合作、交流的愿望。

三、教学的重点和难点

重点：角速度的概念以及角速度与线速度的关系。

难点：角速度的概念以及其单位rad/s（弧度/秒）的含义。

四、教学资源

电脑、投影仪、多媒体课件、自行车等。

五、教学设计思路

本设计包括三部分内容，一是角速度的概念；二是角速度与线速度的关系；三是角速度、线速度与周期、转速的关系。

本设计的基本思路是：以生活生产中常见的转动实例为基础，通过分析、比较得出角速度的概念，继而根据线速度的定义以及数学知识推导出线速度与角速度关系。然后根据周期、转速的含定义导出它们与角速度、线速度的关系式。最后通过对自行车的探索研究，巩固所学知识，感悟物理学在生活、生产等方面的重要作用。

本设计要突出的重点是：角速度的概念以及角速度与线速度的关系。方法是：从观察电风扇的转动入手，根据事实“每个叶片上的不同点线速度虽不一样，但我们仍说各点转的一样快”，帮助学生明白仅仅用线速度描述圆周运动的快慢是不够的，还需要用与转动有关的物理量来更全面地描述圆周运动的快慢，从而真正理解引入“角速度”的意义。教学时，对于角速度的定义要注意引导学生与线速度的定义进行比较。在导出角速度和线速度的关系式v ＝ωr后，要注意结合实例讨论，引导学生认识角速度和线速度的区别与联系。

本设计要突破的难点是：角速度的概念以及其单位rad/s（弧度/秒）的含义。让学生正确理解角速度的概念（同上）。而正确理解角速度单位的方法是：从弧度的含义出发，通过实例认识rad/s的物理意义，并用练习进行巩固。

本设计强调：新知识与已学知识、新知识与生产、生活、科技实例的联系，重视概念的形成过程以及伴随这一过程的的科学方法。

完成本设计的内容约需2课时。

六、教学流程

1．教学流程图

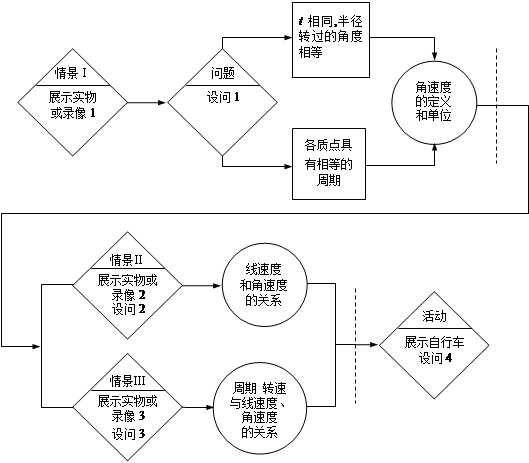
2．流程图说明

情景Ⅰ 展示实物或录像带

通过设问1“匀速转动物体上的各质点，在转动过程中，它们的速度大小是不同的，那么它们具有那些共同特征呢？”指导学生观察讨论，得出“各质点具有相同的转动周期和各质点所在半径在单位时间内转过的角度相同”的结论。让学生看出仅仅用线速度来描述圆周运动的快慢是不够的，还需要用与转动有关的物理量更全面地描述圆周运动的快慢。

情景Ⅱ 用课件或录像2，设问2

设问2“如果已知某电风扇的转动角速度为100π弧度/秒，那么叶片上距中心轴0.30米处的一点A线速度多大？”接着利用实例以及“线速度”、“弧度”的概念引导学生推导角速度与线速度的关系v＝ωr；ω＝v/r 。

情景Ⅲ 展示实物或录像3，设问3

与情景Ⅱ以及设问类似，最好利用实例以及周期、转速、线速度、角速度的物理意义来引导学生推导它们之间的关系，这样有利于学生的理解与记忆。

活动 展示自行车，设问4

最后一部分是对自行车的探索研究，其主要内容是：

（1）自行车正常行驶过程中有那些部件做圆周运动？

（2）这些部件上的点其线速度角速度有何关系？

（3）自行车的行驶速度与那些因素有关？

3．教学的主要环节

根据本节知识的形成过程，本教学设计将本课课时分为三个主要环节：参见教学流程图。

七、教案示例

情景展示1：展示匀速转动的电风扇（实物或录像）

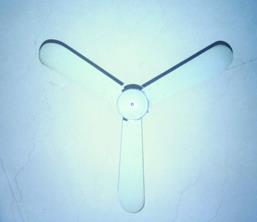
师：通过上一节课的学习我们已经知道可用“线速度”描述质点作圆周运动的快慢。匀速转动的电风扇上各质点的线速度大小是不同的，那么它们具有那些共同特点呢？

情景观察提示：

在翼片半径连线上任意取两点，在转过一周时，它们的线速度大小怎样？转过的角度怎样？

生：学生观察讨论后得出：“各质点所在半径在相同时间内转过的角度相同”以及“周期相等”。

师：可见，仅仅用线速度来描述圆周运动的快慢是不够的，还需要用与转动有关的物理量更全面地描述圆周运动的快慢。

板书 （一）角速度

定义：当质点做圆周运动时，质点所在半径转过的角度与所用时间t的比值就是角速度的大小。

公式：ω＝θ/t 单位：rad/s（弧度/秒），360°＝2πrad。

例题：计算地球和月亮公转的角速度

ω_月＝2π/T_月 ＝2π/28×24×3600 rad/s＝2.6×10^-6rad/s

ω_地＝2π/T_地 ＝2π/365×24×3600 rad/s＝1.99×10^-7rad/s

∴ω_地＜ω_月

通过计算知道，书中所提到的地球和月球的争论是没有结论的。比较运动得快慢，要看比较线速度还是角速度，不能简单说谁快谁慢。

情景展示2：展示匀速转动的电风扇（实物或录像或其他作圆周运动的物体）。

师：如果已知某电风扇的转动速度为100πrad/s，那么叶片上距转轴0.30米处的质点A的线速度v_A大小是多少？

生：让学生讨论。

师：复习线速度的定义（v＝s/t ）；

复习弧度的含义；

指导学生推导：v＝s/t ＝θr/t ＝100π×0.3/1 m/s＝30πm/s

师设问：如果已知某质点运动的角速度为ω,它距轴的距离为r，那么它的线速度v如何求？

生：v＝s/t ＝θr/t ＝ωr

板书 （二）角速度与线速度关系v＝ωr，ω＝v/r

师设问：有人根据v＝ωr和ω＝v/r ，说ω与r成正比，v与r成反比，你认为对吗？

生：学生讨论，交流得出结论。

情景展示3：（同情景2）

师：如果已知某电风扇的周期为T（或每分钟转n转），那么距离转轴为r的质点的线速度、角速度如何求？

生：学生讨论，教师指导，学生做好发言准备。

交流：选一位学生到讲台讲解，并允许下面的学生做补充纠正！

板书 （三）v ＝ 2πr/T ，ω＝2π/T

                 v＝2πnr/60 ，ω＝2πn/60

（T为周期，n为转速，即每分钟物体转的转数）

探索研究

结构介绍：自行车主要传动部件：牙盘、飞、脚踏曲柄、链条。

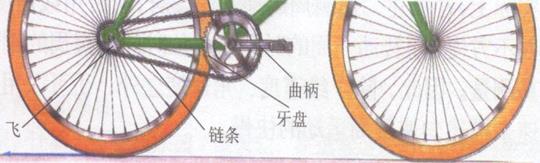
讨论a：自行车正常行驶过程中有那些部件做圆周运动？

讨论b：自行车中脚踏板中心点与后轮边缘上任一点的线速度、角速度、周期、转速关系怎样？

讨论c：自行车的行驶速度与那些因素有关？

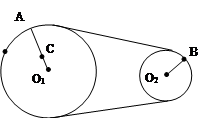
例：如图所示，在皮带转动中，如果大轮O₁的半径R为40cm，小轮O₂的半径r为20cm。A、B分别为O₁、O₂两个传动轮边缘上的一点，C为大轮O₁上的一点，距轴线O₁的距离为R/4 ，则A、B、C三点的线速度大小之比v_A∶v_B∶v_C＝________，角速度大小之比ω_A∶ω_B∶ω_C＝________，周期之比T_A∶T_B∶T_C＝_______，转速之比n_A∶n_B∶n_C＝_________。

作业

略。

发布时间：2013/5/17 上午7:44:14  阅读次数：3869