地球上山高极限的数量级估计

据说，在国外某华裔中餐馆老板想制作一块一米立方的豆腐为广告，以招揽生意，但由于豆腐瘫软而始终未果．这是可以理解的，但坚硬岩石太高了也会瘫软，你相信吗？请看下面的例题。

估计一下地球上山高的极限。

解：假设山峰的高度主要受岩基的刚度所限制。若山太高，加在岩基上的压强过大，它将从弹性形变过渡到塑性形变，开始流动。计算这一过程所需能量时，不妨认为固态岩基先升温至熔点，熔化后又过冷地降到原有温度。设固态和过冷液态的比热差不多，于是升温和降温过程中与外界的能量交换大体相抵，唯一要计算的是熔解热，能量的来源是因山高下降所释放的重力势能。

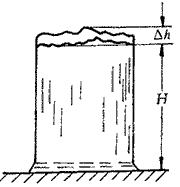
如图所示，设山是上下同样粗的柱体，下降距离Δh时势能减少 AρgHΔh（A 为山的横截面积，ρ 为其密度，g 是重力加速度）。与此同时，熔化的岩石吸热 AΔhρΛ_m／μ（μ 为岩石的摩尔质量）。令两者相等，作为山高极限的条件，于是我们有 AρgHΔh ＝ AΔhρΛ_m／μ 得

H＝Λ_m／μg

可以认为岩石的主要成份是 SiO₂，因此 μ ＝ 60g／mol，由表查得 SiO₂ 的 Λ_m＝2.04kcal／mol＝8540J／mol，代入上式，得山高的上限 H ＝ 14.5 km。

世界上最高的山峰珠穆朗玛峰高 8848 m，确小于此限，但属同一数量级。古诗中常有山高"万仞"的说法，如：

黄河远上白云间，一片孤城万仞山，

羌笛何须怨杨柳，春风不度玉门关。

（唐王之涣《凉州词》）。"仞"是古代的长度单位，具体的大小其说不一，大约是几尺（4 ～ 8 尺），我们取其中，1仞 ≈ 6 尺 ＝ 2 m，则万仞 ≈ 20 km，这数值显然是夸大了。凉州在现今的甘肃省武威县，凉州一带的山是祁连山，它的高度实际上只有海拔 4 km 左右。当然作诗不是大地测量，诗人的浪漫主义谁也不会去责怪。

估计一下月球上山高的上限。

解：月球上的重力加速度为地球上的 1/6，在其它条件相似的情况下，月球上山高的上限大 6 倍，即 84 km，这不到月球半径 1738 km 的 5％。

佛家言：天地从形成到毁灭，谓之一"劫"，或"劫簸"、"劫波"（梵文kalpa的音译）。为了解释这样一段时间有多长，"佛祖"做了多种比噙。佛典《大智度论》曰；"佛以譬喻说劫义。四十里石山，有长寿人，百岁一来，以细软衣拂拭此大石尽；而劫未尽。又四十里大城满芥子，有长寿人，百岁一来取一芥子，芥子尽而劫尚不尽。"这便是"盘石劫"，"芥子劫"之说。我们不妨以"盘石劫"为据估算一下"佛祖"所说的一劫具有怎样的数量级。

40 里折合 20 km，如果以此为山高，数量偏大。按照前面的分析，取山高为 10 km 的数量级，还是合理的。假设此山方圆数百里，其底座面积为（10² km）²，故体积为10⁵km³ ＝ 10²⁰ cm³。岩石（SiO₂）的平均密度小于 3g/cm³，平均摩尔质量 μ ＝ 60g/mol，从而石山内所含物质的摩尔数约为 n ＝（3×10²⁰）/60＝5×10¹⁸mol

现在来估算一下，那位长寿老人每次拂拭中磨损掉多少山石物质。假定衣料与山石间摩擦力为 0.1 N，位移 10 cm，因此作功 10^－2 J。我们不妨认为山石比细软的衣料耐磨 1000 倍，即每次拂拭传递给山石的能量为 10^－5J。典型的共价健化学结合能为 100 kcal/mol ＝ 4.2×10⁵J/mol，即老人每次抹去 10^－5J/（4.2×10⁵J/mol）＝ 2.3×10^－11mol的山石物质。要把整座石山抹平，他需要来 5×10¹⁸/2.3×10^－11 ≈ 2×10²⁹ 次。老人每百年来一次，共历时 2×10³¹ 年。这便是"佛祖"对宇宙寿命的预言。

这是个什么数字？SU（5）大统一理论预言的质子蜕变寿命 τ_p 正合此数！若质子都蜕变掉了，原子核全部瓦解，现在形式的宇宙当然就此毁灭。难道这正是"佛祖"隐喻之所指？不过 IBM 公司协作组的实验已否定了上述结论，他们给出τp的下限是 1.7×10³² 年。这就对了！"佛祖"不是说"大石尽，而劫未尽"吗？

发布时间：2006/7/21 下午7:27:09  阅读次数：8806