第五章 第二节 洛伦兹力

5–19 极光现象
在地球南北两极附近的高空,夜间常会出现美丽灿烂的光辉,这种壮丽动人的光辉叫做极光。如图 5–19 所示就是一张极光照片。大多数极光出现在地球上空 90 ~ 130 km 处。我们该去哪儿才能欣赏到极光呢?目前公认的是在南北纬 67° 附近的两个环带状区域内。纬度低的地方观察到极光的机会很少。
极光现象的产生与带电粒子在磁场中的运动有关。我们已经知道安培力是磁场对通电导体的作用力,而电流是由于电荷的定向运动而形成的。由此我们也可以设想,磁场对运动电荷会有作用力。
如图 5–20 所示的实验装置叫做阴极射线管。阴极射线管的阴极会发射电子。如果在射线管的两极间加上高电压,阴极发射的电子就会向阳极高速运动,形成电子束。利用荧光屏可更清晰地显示出电子束运动的径迹。当电子束周围没有磁场时,电子束沿直线前进;当蹄形磁体移至射线管旁边时,电子束运动的径迹就发生了弯曲,如图 5–21 所示。电子束在磁场中会发生偏转,运动方向改变说明受到力的作用。这表明电子受到了磁场力的作用。人们把运动电荷在磁场中所受到的力以荷兰物理学家洛伦兹(H. A. Lorentz, 1853—1928)的姓氏命名,称为洛伦兹力(Lorentz force)。
图 5–20 阴极射线管结构
图 5–21 电子束在磁场中偏转
实验和理论都表明,电荷量为 q 的粒子以速度 v 定向移动时,如果电荷运动方向与磁场方向垂直,那么带电粒子所受的洛伦兹力大小为
即电荷垂直于磁场方向运动时,磁场对运动电荷的作用力 f 的大小等于电荷量 q、速率 v 和磁感应强度 B 三者的乘积。
金属导体中自由电子的定向运动形成电流。洛伦兹力作用在载流导线中运动的自由电子上,使其侧向偏转,导致导线侧向负电荷积累。导线另一侧相应积累原子实的正电荷(设为 + e),由此在导线中形成侧向电场。这一电场对电子的作用力和洛伦兹力方向相反,阻止电荷继续积累。直到侧向电场力和洛伦兹力等值反向,彼此
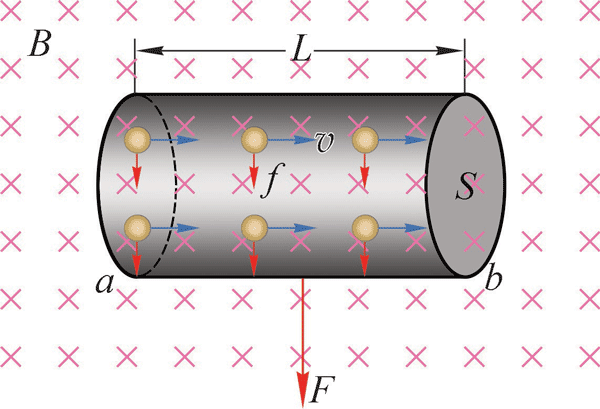
5–22 导线内运动电荷的洛伦兹力宏观表现为安培力
平衡相消;电荷不再继续积累。每个电子所受电场力的反作用力均作用于导线,大小与方向都和电子所受的洛伦兹力相同,其合成就是安培力,从而可从安培力的公式出发推导出洛伦兹力的表达式。
如图 5–22 所示,在磁感应强度为 B 的匀强磁场中,垂直于磁场方向放入一段长为 L = vt,截面积为 S 的通电导线。设每单位体积的导线中有 n 个自由电子,每个电子的电荷量是 e,电子定向移动的速度是 v。
根据以上条件可得出通过导线截面的电荷量与时间之比,即电流
再由安培力公式 F = BIL 和这段导体中运动电子的总数 N = nSL,可求得每一个运动电荷所受的洛伦兹力
既然洛伦兹力与安培力存在一定关系,我们曾经用左手定则判断安培力的方向,洛伦兹力的方向能否同样用左手定则来判断呢?
如图 5–23 所示,用一个蹄形磁体在阴极射线管中电子束的路径上施加磁场,观察不同方向的磁场对电子束径迹的影响,从而判断运动的电子在磁场中的受力方向。观察并记录磁场方向和电子束的偏转方向。

图 5–23 阴极射线在磁场中的偏转
图 5–24 用左手定则判断洛伦兹力的方向
洛伦兹力的方向也可以用左手定则来判断:如图 5–24 所示,伸开左手,让大拇指跟其余四指垂直,并且都与手掌在同一平面里;把左手放入磁场中,让磁感线垂直穿入掌心,四指指向正电荷运动的方向,那么拇指所指的方向就是正电荷所受洛伦兹力的方向。如果负电荷在磁场中运动,那么四指的方向必须和负电荷的运动方向相反,因为电流的方向规定为正电荷的运动方向。拇指所指的方向就是负电荷所受洛伦兹力的方向。上面的自主活动表明,洛伦兹力的方向与电子束的偏转方向相同,洛伦兹力就是运动电荷受到的磁场对它的作用力。
图 5–25 粒子束进入匀强磁场
示例 如图 5–25 所示,一束粒子包含有质子(带正电)、电子(带负电)和光子(不带电)三种粒子。粒子束中的粒子沿水平向右的方向射入垂直纸面向里的匀强磁场中。请分析并描述粒子束进入匀强磁场后的偏转情况。
分析:根据粒子束中的粒子所带的电荷和左手定则即可
判断。
解:粒子束内的光子不带电,不受磁场的任何影响。质子和电子带有电荷,会受洛伦兹力作用。粒子束内的光子不发生偏转保持原有速度匀速前进;粒子束内的质子带正电,由左手定则可知所受洛伦兹力向上,所以射入匀强磁场后质子束向上偏转;粒子束内的电子带负电,使用左手定则时,四指方向应与电子运动方向相反,可判定电子束进入匀强磁场后向下偏转。
电荷在电场中一定受到电场力的作用,运动电荷在磁场中是否一定受到洛伦兹力的作用?
在磁场中运动的电荷因受到洛伦兹力作用,运动方向会发生偏转。这一点对地球上的生命来说十分重要。地球时刻都面临着宇宙空间大量高能粒子流的轰击(这些粒子流总称为“宇宙线”),尤其是离我们最近的恒星太阳辐射出的高能粒子流,又叫做太阳风,对地球影响重大。这些高能粒子流(主要是由电子、质子组成)如果都到达地球,将给地球上的生物带来危害。幸亏地球周围存在地磁场,地磁场改变宇宙射线中带电粒子的运动方向,使其中的大部分不致到达地球,从而保护了地球上的生物。
在低纬度区域,来自太阳风的高能带电粒子由于受到地球地磁场的洛伦兹力的作用,发生偏转未能接近地球。在高纬度区域,来自太阳风的高能带电粒子有部分沿着地磁场方向运动接近地球,可达到离极区地表 80 km 以上的高层大气层。这些带电粒子(主要是电子)与这一高度范围的大气原子与分子碰撞使后者受到激发而发光,由于不同元素的气体受轰击后发出不同颜色的光,从而产生绚丽的极光。
静止电荷产生电场,仅受库仑力作用。运动电荷除了会产生电场,还会产生磁场。它不仅受到库仑力的作用,还会受到洛伦兹力的作用。因此,我们也可以从运动电荷所受的洛伦兹力出发来定义磁感应强度,即 B =
- 电子以 6×106 m/s 的速率垂直射入磁感应强度为 0.5 T 的匀强磁场中,电子受到的洛伦兹力的大小为何?如果电子射入磁场时的速度 v 与磁感应强度 B 的方向间的夹角是 180°,则电子所受的洛伦兹力大小为何?
- 如图 5–26 所示,试判断运动电荷在磁场中所受洛伦兹力的方向。
图 5–26
- 如图 5–27 所示,阴极射线管(A 为阴极)放在蹄形磁体的 N、S 两极间,阴极射线管的 A、B 两端分别通过导线连接到直流高压电源的哪个电极?若无磁体,电子的运动方向如何?磁体如图示情境放置,电子束运动轨迹的偏转情况如何?
图 5–27
- 如果一个电子在通过空间某区域时不偏转,是否能肯定该区域中没有磁场?如果一个电子在通过空间某区域时发生侧向偏转,是否能肯定该区域中存在着磁场?试说明理由。
- 某区域存在一竖直向上的匀强磁场,磁场的磁感应强度大小为 1.2×10−3 T。动能为 5.3 MeV 的质子由南向北水平通过磁场区域,则质子受到的洛伦兹力的大小和方向如何?(质子质量为 1.67×10−27 kg,忽略地球磁场)
- 如图 5–28 所示,偏转极板间存在匀强电场,匀强电场的电场强度为 1.5 kV/m,方向竖直向下;线圈系统(图中未显示)产生的匀强磁场的磁感应强度为 0.4 T,方向垂直纸面向里。若灯丝发射的电子能沿直线匀速通过电场和磁场区域,那么,电子运动的速度大小是多少?(忽略电子所受重力)
图 5–28
本节编写思路
本节以美丽的极光现象作为情境,激发学生学习洛伦兹力的兴趣。根据磁场对电流有力的作用,而电流又是由电荷的定向移动形成,引导学生猜想磁场对运动电荷有力的作用,并通过阴极射线在磁场中偏转的演示实验验证。学会计算洛伦兹力的大小。“拓展视野”供学习能力较强的学生认识安培力是作用在导线内所有运动电荷上的洛伦兹力导致的宏观表现。通过实验,能应用左手定则判断洛伦兹力的方向。在高纬度区域,来自太阳风的高能带电粒子有部分沿着地磁场方向运动进入极区附近的大气层后使大气分子受激发而发光,由此解释节首图的极光现象。
本节注重在呈现知识时创设学生积极参与、乐于探究、勤于思考的学习情境,体会模型建构和演绎推理的方法,增强科学探究能力。本节注意为学生的自主学习搭建平台,培养和发展自主学习能力。
正文解读
阴极射线管的阴极端连接直流高压电源的负极,阳极端连接电源的正极。电子由阴极端向阳极端运动。这个演示实验可让肉眼看不见的电子显现出径迹,让学生观察磁场可使电子径迹发生偏转的现象,从而激发其好奇心和求知欲。
对于电荷运动方向与磁场方向不垂直情况下洛伦兹力大小的计算,可根据学生的学习能力来确定是否拓展。
此处设置“拓展视野”,是为了使学生了解通电导线受到的安培力实际是导线内所有运动电荷所受洛伦兹力的宏观表现。洛伦兹力表达式 f = evB 是在导线与磁场垂直的情况下导出的,这一表达式仅适用于电荷运动方向与磁场垂直的情况。
如果洛伦兹力和安培力的关系作为课堂讲授内容,应说明洛伦兹力和安培力作用的对象不同:洛伦兹力作用于带电粒子(如电子),安培力作用于通电导线。
教学过程中这个活动是演示实验(有条件的学校应尽可能安排为分组学生实验),目的是:
(1)认识洛伦兹力。认识电子束的磁偏转,提升磁场的物质观和相互作用观。
(2)经历得出洛伦兹力、磁场和电荷的运动三者方向关系的过程,体会科学猜想、逻辑思维、实验验证和归纳讨论。
用一个蹄形磁体在阴极射线管电子束的路径上施加磁场,观察不同方向的磁场对电子束径迹的影响,从而判断运动的电子在磁场中的受力方向。观察并记录磁场方向和电子束的偏转方向。
由电子束的偏转情况确定洛伦兹力的方向。填写数据记录表,表中的方向用“向上”“向下”“向左”“向右”“垂直纸面向里”或“垂直纸面向外”填写。
演示实验不仅能够让学生“看到”洛伦兹力的存在,而且可以通过实验发现洛伦兹力的方向与磁场方 向和电荷的运动方向都有关系,从而探究得到洛伦兹力、磁场和电荷运动方向三者间的关系。
|
实验序号 |
电子运动方向 |
磁场方向 |
电子束的偏转方向 |
|
1 |
向右(A→B) |
|
|
|
2 |
向右(A→B) |
|
|
电场和磁场都可以对带电粒子发生作用,此处设置“大家谈”,是为了比较这两种场对带电粒子的作用有何差异。运动电荷在磁场中不一定受到洛伦兹力的作用。如电荷运动方向与磁场方向在同一直线上,则运动电荷不受洛伦兹力的作用。
极光的颜色由大气的成分以及入射高能带电粒子的能量大小决定。
此处设置“拓展视野”,是为了通过磁感应强度的不同定义方式,更深刻地认识磁感应强度和比值定义物理量的方法(详见本节资料链接)。必修三教材中用电流元在磁场中受力来定义(B =
1 T = 1
问题与思考解读
1.参考解答:运动电荷受到的洛伦兹力大小为 f = qvB = 1.6×10−19×6×106×0.5 N = 4.8×10−13 N。
如电荷运动方向与磁场方向在同一直线上,运动电荷受到的洛伦兹力大小为零。
命题意图:会计算洛伦兹力的大小。
主要素养与水平:运动与相互作用观念(Ⅱ);科学论证(Ⅱ)。
2.参考解答:竖直向上,竖直向上,垂直纸面向外。
命题意图:运用左手定则判断洛伦兹力的方向。
主要素养与水平:运动与相互作用观念(Ⅱ);科学推理(Ⅰ)。
3.参考解答:阴极射线管的 A 端连接直流高压电源的负极,B 端连接电源的正极,电子的运动方向由 A→B,电子束运动轨迹向上偏转。
命题意图:运用左手定则判断洛伦兹力的方向,解释电子束在磁场中偏转的原因。
主要素养与水平:运动与相互作用观念(Ⅲ);科学推理(Ⅱ)。
4.参考解答:电子通过空间某区域时不偏转,该区域不一定没有磁场。如磁场方向与电子运动方向在同一条直线上,运动电子不受洛伦兹力作用故不发生偏转。也有可能空间区域内既存在磁场也存在电场,电场力和洛伦兹力平衡所以不发生偏转。
电子在通过空间某区域发生侧向偏转,可能是电子通过电场区域受到电场力的作用,也可能是电子通过磁场区域受到洛伦兹力的作用,所以该区域中不一定存在磁场。
命题意图:将静电场知识和磁场知识相关联分析带电粒子偏转的原因,电场力和磁场力都能使带电粒子发生偏转。
主要素养与水平:运动与相互作用观念(Ⅲ);科学推理(Ⅱ)。
5.参考解答:
Ek =
v =
f = qvB = 1.6×10−19×3.19×107×1.2×10−3 N = 6.12×10−15 N
洛伦兹力的方向:水平向东。
命题意图:针对匀强磁场与带电粒子运动方向垂直的情况,会计算带电粒子所受洛伦兹力的大小,能 判断洛伦兹力的方向。
主要素养与水平:能量观念(Ⅱ);科学推理(Ⅲ);科学论证(Ⅱ)。
6.参考解答:忽略电子所受重力,运动电荷在电场中受到电场力 qE,竖直向上。运动电荷在磁场中 还受到洛伦兹力 qvB,竖直向下。电子匀速的通过电场和磁场区域,合力为零
qE = qvB
v =
命题意图:将静电场知识、磁场知识与力学知识相关联,培养学生综合分析问题和解答实际问题的能力。
主要素养与水平:运动与相互作用观念(Ⅲ);科学推理(Ⅲ);科学论证(Ⅱ)。
资料链接
洛伦兹
亨德里克·安东·洛伦兹(1853— 1928),荷兰物理学家,于 1881 年当选荷兰皇家艺术与科学学院院士,并与彼得·塞曼共同获得 1902 年诺贝尔物理学奖,同时还曾担任多国科学院外籍院士。洛伦兹以其在电磁学与光学领域的研究工作闻名于世。他通过连续电磁场以及物质中离散电子等概念得到了经典电子理论。
洛伦兹在《麦克斯韦电磁理论及其在运动物体中的应用》中首次阐述了电子理论。他在其中还给出了电磁场对运动电荷的作用力,即洛伦兹力表达式。洛伦兹以真空(以太)中宏观的麦克斯韦方程组以及其他唯象方程为出发点,研究了物质电磁作用的微观机制。洛伦兹的电子理论很好地解释了物质中的一系列电磁现象以及物质在电磁场中运动的一些效应,这与现在的电磁场的概念十分接近。洛伦兹对以太与物质加以明确的区分,它们并不能直接产生力学联系,而只能通过电磁力相互作用。在电子理论的基础上,他还发展了运动介质中的电动力学,包括提出物体在其运动方向上会发生长度收缩的假说、引入了“局部时”的概念、获得了质量与速度之间的关系并构造了表述不同惯性系间坐标和时间关系的方程组(洛伦兹变换)。洛伦兹的研究工作后来成为狭义相对论与量子物理的基础。此外,洛伦兹在热力学、分子运动论、广义相对论以及热辐射理论等方面也有建树。
用通电试探线圈受到的力矩来定义磁感应强度 B
静电场可以用试探电荷在电场中各点受到的作用力来研究,那么研究磁场也需要引进一个可用来试探的物体。用电流元给磁感强度下定义有缺点,因为不存在电流元。磁场除对电流元和运动电荷有作用力外,对通电线圈有力矩的作用。选用不同的试探磁场的物体,也就有不同比值定义法得到的磁感应强度 B。
下面我们以匀强磁场对通电试探线圈的作用为例来进行说明。如图 7(a)所示,矩形小线圈的 ab 边长为 l1,bc边长 l2,小线圈面积为 S,匀强磁场的磁感应强度为 B,线圈中的电流为 I,磁矩矢量与磁感应强度间的夹角为 φ。
ad 边和 bc 边所受到的安培力 F1 = F1ʹ = BIlsin(π − φ) = BIlsinθ,F1 和 F1ʹ 大小相等、方向相反、在同一直线上,合力为 0。
ab 边和 dc 边所受到的安培力 F2 = F2ʹ = BIl2,F2 和 F2ʹ 大小相等、方向相反、不在同一直线上,形成力偶。
如图 7(b)所示,通电线圈所受的磁场力的力矩为 M = F2
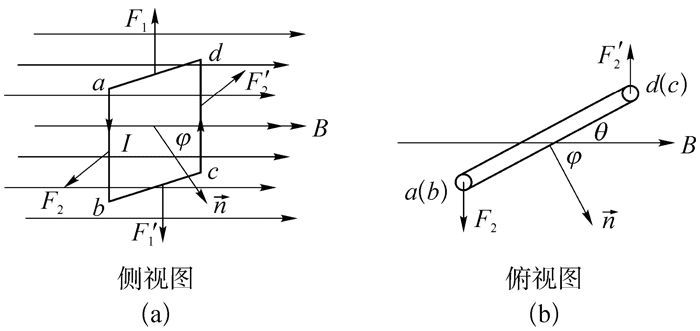
图 7
利用通电试探线圈来检测磁场时,同样可以用比值定义法来定义磁感应强度 B 的大小为 B =
用磁力矩定义磁感应强度 B 同样适用于非均匀磁场和任意形状的线圈。因为只要试探线圈线度足够小,线圈范围内磁场可视为均匀,试探线圈的通电电流小就不影响磁场原有性质。
发布时间:2022/6/13 下午10:53:50 阅读次数:8740
