本课件可用来演示线速度、向心力的方向，线速度和角速度的定义。。

课本内容

对应上海科技出版社2007版《物理 高中一年级第二学期》教材第3、4、6页：

向心力与线速度方向

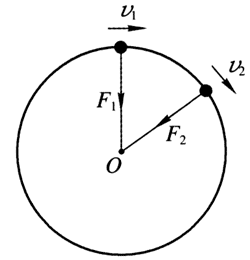
如果质点做圆周运动，那么质点所受的合外力或者合外力的某个分力一定指向一个固定的圆心。这个不断改变质点运动方向，并始终指向圆心的力叫做向心力。在图4-9中，$F_1$和$F_2$表示质点在不同位置所受的向心力。可见，受到向心力作用是质点做圆周运动的条件。

线速度的定义

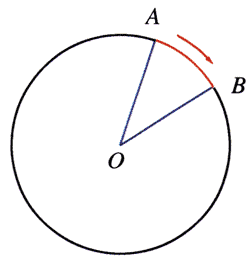
因为圆周运动的轨迹是曲线，如图4-10所示，圆周运动的速度大小要用质点所通过的A、B两点之间的圆弧长度$s$与所用时间$t$之比来表示，这个速度叫做线速度。

线速度用符号$v$表示，则有：

$$v= \frac{s}{t}$$

线速度的单位是m/s。

角速度的定义

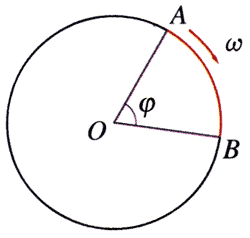
在图4-15中，质点由A点沿圆周运动到B点，质点所在半径转过的角度为$\varphi$，所用的时间为$t$，用$\varphi$除以$t$，就是质点所在半径每秒转过的角度，也就是质点的角速度的大小。

角速度用$\omega$表示，则有：

$$\omega = \frac{\varphi}{t}$$

在国际单位制中，角度的单位是rad（弧度），时间的单位是s，角速度的单位是rad/s，读作弧度每秒。

使用方法

1、点击左下角播放按钮，可以使小球做匀速圆周运动，选中复选框可以显示速度和向心力矢量。

2、选中"显示通过的弧长s"并拖动时间滑动条可以展示线速度的定义。

3、选中"显示半径转过的角度φ并拖动时间滑动条可以展示角度的定义。