重心与质心

重心与质心是物理学中两个重要概念，由于它们只有一字之差，运用中很容易混淆。其实，“重心”和“质心”这两个概念有着不同的内涵和外延，是两个截然不同的力学概念。

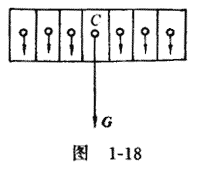首先看重心，任何物体都可以看作是由很多微粒所组成，每个微粒都受到竖直向下的重力的作用，由于地球很大，这些力可认为彼此平行。因此，又可以说任何一个物体都受到很多的平行力——物体的各微粒所受的重力的作用。所有这些重力的合力就等于整个物体的重力，它可以根据平行力的合成法则来求得。这些平行力的合力作用点就叫做物体的重心（如图1－18的 C 点）。

由此可见，重心必须依赖重力而存在。实际上，重心反映了重力“三要素”中的“作用点”要素，因此，可以说重心是重力概念的一个派生概念。根据重心的定义，严格地讲，在地面上方的物体有重心的充分必要条件是作用在它各部分的重力的作用线是相互平行的。在地面上方的大物体不存在以上意义的重心 。可见，重心概念只对地球附近处受到地球引力的一切小物体有意义。另外，根据重心定义可以知道，重心是一个定点，与物体所在的位置和如何放置无关。均匀物体的重心只跟物体的形状有关，规则形状的均匀物体的重心就在它的几何中心。如均匀直棒的重心就在它的中点，均匀圆板的重心就在圆板的圆心，均匀球体的重心就在它的球心等等。几何上之所以把三角形的二条中线的交点称为重心，就是因为此交点实为物理上的重心位置。形状不规则、质量分布又不均匀的物体的重心位置，除与物体的形状有关外，还与物体内部质量的分布情况有关：找物体重心除用计算法外还可用实验悬挂法；用线悬挂物体（A 点），平衡时，物体重心一定在悬挂线（或其延长线）上，然后把悬挂点换到物体上另一点（B 点），再使之平衡，则物体的重心又一定在新的悬挂线（或其延长线）上，前后两次悬挂线的交点 C 就是所求物体的重心位置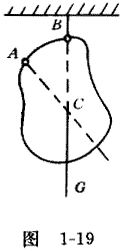，如图 1－19 所示。有一点必须注意，即物体的重心可以不在物体内部，关于这点，请读者自行举例。

在物理学上，把物体的平衡程度称稳度，而稳度的大小与物体的重心有紧密的联系。一般来说，重力相同，底面积相同，重心高的物体稳度小；重力相同，底面积不同，而重心高度相同的物体，底面积小的则稳度小。杂技演员表演成功的关键往往就是掌握好自己的重心。

下面我们再来看质心。众所周知，当物体不是作单纯的平动而是作比较复杂的运动时，物体上的各点运动状态（速度与加速度）不相同。但是，我们总可以把物体看成质点组来分析、处理，即想象把物体分成许多的质元，在每一质元范围内，速度和加速度是相同的。于是，对于每个质元，按牛顿第二定律有运动方程：

\[{m_i}{{\bf{a}}_i} = {{\bf{F}}_i} + \sum\limits_j {{{\bf{f}}_{ij}}} \tag{1}\label{1}\]

式中 a_i 是第 i 个质元 m_i 的加速度，F_i 是第 i 个质元 m_i 受到来自物体外部的外力，\({\sum\limits_j {{f_{ij}}} }\) 是 m_i 受到除它自己以外的物体上其他质元的作用力之和。对于物体中每一质元，均有类似（1）式的运动方程。把所有质元的运动方程加起来，可得：

\[{m_i}{{\bf{a}}_i} = \sum\limits_i {{F_i}}  + \sum\limits_i {\sum\limits_j {{f_{ij}}} } \tag{2}\label{2}\]

令 F＝ F_i（物体所受外力的“矢量和”或“主矢”），并注意到内力和等于零，则（2）式可化为：

\[\sum\limits_i {{m_i}{{\bf{a}}_i} = {\bf{F}}} \tag{3}\label{3}\]

显然，若物体作平动，则上式 a_i 是一常矢，不妨暂定为 a，于是，（3）式可进一步改写为：

\[m{\bf{a}} = {\bf{F}}\tag{4}\label{4}\]

（4）式中 m ＝ \(\sum\limits_i {{m_i}} \)，为物体的总质量。然而，现在我们研究的物体运动并非平动，故（3）式不能写成（4）式。不过，我们可换一种思想来考虑问题。

我们能不能找到一个能代表物体整体运动的点 C？譬如说物体中（或物体外）的某一点，它对于物体的相对位置是固定的，并随物体一起运动，且这一点的加速度 a_C 满足下式：

\[{{\bf{a}}_C} = \frac{{\bf{F}}}{m}\tag{5}\label{5}\]

即 C 点的加速度相当于把物体的全部质量 m 集中于 C 点，合外力 F 也是作用于 C 点时所产生的加速度。于是，由（3）式得知 C 点的加速度应满足下式：

\[{{\bf{a}}_C} = \frac{{\sum\limits_i {{m_i}{{\bf{a}}_i}} }}{m}\tag{6}\label{6}\]

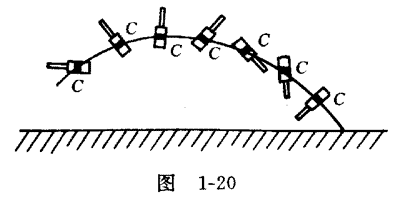
事实上，这样一个 C 点是存在的，例如观察手榴弹在重力作用下的运动，我们可发现，手榴弹总是绕着一个确定的点 C 翻转，而这个 C 点在空中的轨道是一条抛物线（忽略阻力），如图 1－20 所示。就是说，在手榴弹这一物体中，有一个特殊点 C，手榴弹在重力作用下运动的整体移动可以由这个点 C 的运动代表。符合上述要求的这个 C 点就称为物体的质量中心，或简称质心。

不论是形状固定的物体还是空间范围可变的质点组中都可以找到一个质心，可用它的运动代表物体或质点组的整体移动。相对于坐标原点在某一 O 点的坐标系来说，质心的矢径应为：

\[{{\bf{r}}_C} = \frac{{\sum\limits_i {{m_i}{{\bf{r}}_i}} }}{m}\tag{7}\label{7}\]

相对于直角坐标系来说，因为 r_C＝x_Ci＋y_Cj＋z_Ck。所以质心的坐标 x_C、y_C、z_C 分别为

\[\begin{array}{l}{x_C} = \frac{{\sum\limits_i {{m_i}{x_i}} }}{m}\\{y_C} = \frac{{\sum\limits_i {{m_i}{y_i}} }}{m}\\{z_C} = \frac{{\sum\limits_i {{m_i}{z_i}} }}{m}\end{array}\tag{8}\label{8}\]

可以证明由（7）式或（8）式所确定的质量中心的加速度确定满足（6）式：将（7）式左右两边对时间微分两次，可得质心的加速度：

\[{{\bf{a}}_C} = \frac{{{{\mathop{\rm d}\nolimits} ^2}{{\bf{r}}_C}}}{{{\mathop{\rm d}\nolimits} {t^2}}} = \frac{{\sum\limits_i {{m_i}{{\bf{a}}_i}} }}{m} = \frac{{\bf{F}}}{m}\tag{9}\label{9}\]

（9）式就是（5）式或（6）式。所以，（7）式所表示的质心的确存在，它的加速度符合（5）式的要求。（9）式表明：对于物体（或质点组）有一个质量中心（质心），它的运动好像是一个质点的运动，这个质点的质量就等于物体的全部质量，受到的力就是物体所受到的所有外力的矢量和。可见，质心的运动与内力无关，若外力的矢量和等于零，则物体的质心静止或作匀速直线运动。质心除具有上述几个重要性质外还有很重要的性质。例如，若外力作用线不通过质心，则物体既作平动又作转动；若外力的作用线通过质心，则物体只作平动而不发生转动。又如，经计算可知，不管物体的形状如何，其重力势能总可以用其质心高度乘以物体的总质量和重力加速度来表示。

原则上，任何物体的质心均可用（7）式来求得（严格讲，对于质量连续分布的物体质心应用与（7）式相应的积分公式来求）。对于形状规则、质量分布均匀的物体来说，质心就在其几何中心。但必须指出，质心与重心一样，并非一定要在物体内部，它可以在物体内部，有时也可以在物体外部。最后，还有一点要注意，质心作为位置矢量，其矢径与参考点的选择有关。但是，可以证明，对于一定的物体或质点组，质心相对于物体或质点组的位置完全由物体或质点组的质量分布决定。

可见，重力与质量的意义不同，重心与质心的意义也不同，如前所述，重心与物体所受的重力相联系，它实际上是重力组成的平行力系的中心，而质心与物体的质量分布相联系，它可视为一个特殊的“质点”，这个“质点”的质量同整个物体的质量相等，这个“质点”的位置由前述（7）式决定。根据（7）式，质心实际上是组成物体各质元的矢径ri的加权平均中心，所取的权重就是该质元的质量。显然，物体的质心只与物体各部分质量分布有关，而与重力无关。所以，质心概念对处于任何位置的任何物体都具有意义。

一般情况下，质心与重心的位置不重合。尺寸不十分大的物体放在重力场中，它上面各质元所在处的重力加速度 g 相同。这时物体的质量分布和物体的重力分布是一致的，物体的质心和重心位置重合。复杂物体重心位置可以由实验（悬挂法）测定，因此，利用质心与重心重合这一点也可以由实验测定复杂物体的质心位置。如果物体各处的重力加速度不同，则质心和重心不再重合，而且当物体或质点组与地球相距极远时，可以认为它们不再受重力，重心也就失去了意义，但是质心的概念却仍然有效。由此可见，质心的概念比重心的概念更具有普遍的意义。

发布时间：2009/4/20 下午3:16:53  阅读次数：68864